| Title: | Logarithm |
| Original Title: | Logarithme |
| Volume and Page: | Vol. 9 (1765), pp. 630–633 |
| Author: | Jean-Baptiste le Rond d'Alembert (biography) |
| Translator: | David Fleming |
| Subject terms: |
Arithmetic
|
| Original Version (ARTFL): | Link |
| Rights/Permissions: |
This text is protected by copyright and may be linked to without seeking permission. Please see http://quod.lib.umich.edu/d/did/terms.html for information on reproduction. |
| URL: | http://hdl.handle.net/2027/spo.did2222.0003.598 |
| Citation (MLA): | d'Alembert, Jean-Baptiste le Rond. "Logarithm." The Encyclopedia of Diderot & d'Alembert Collaborative Translation Project. Translated by David Fleming. Ann Arbor: Michigan Publishing, University of Michigan Library, 2017. Web. [fill in today's date in the form 18 Apr. 2009 and remove square brackets]. <http://hdl.handle.net/2027/spo.did2222.0003.598>. Trans. of "Logarithme," Encyclopédie ou Dictionnaire raisonné des sciences, des arts et des métiers, vol. 9. Paris, 1765. |
| Citation (Chicago): | d'Alembert, Jean-Baptiste le Rond. "Logarithm." The Encyclopedia of Diderot & d'Alembert Collaborative Translation Project. Translated by David Fleming. Ann Arbor: Michigan Publishing, University of Michigan Library, 2017. http://hdl.handle.net/2027/spo.did2222.0003.598 (accessed [fill in today's date in the form April 18, 2009 and remove square brackets]). Originally published as "Logarithme," Encyclopédie ou Dictionnaire raisonné des sciences, des arts et des métiers, 9:630–633 (Paris, 1765). |
Logarithm . Number in an arithmetic progression, which corresponds to another number in a geometric progression.
To understand the nature of logarithms in a suitably clear and distinct manner, let us take these two types of progression that have given birth to these numbers; that is, the geometric progression , and the arithmetic progression : let us then suppose that the terms of the one are directly set over the terms of the other, as one sees in the following example:
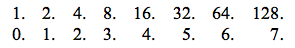
in this case, the numbers in the lower progression, which is arithmetic, are what one calls the logarithms of the geometric progression that is above it; that is to say that 0 is the logarithm of 1, 1 is the logarithm of 2, 2 is the logarithm of 4, and thus as follows.
These logarithms were invented to make the process of calculation more expeditious, as one will see below.
The word logarithm is made of the Greek words λόγος, reason , and ’άριθµόρ, number ; that is to say, reason of numbers .
Now, so that one understands the doctrine and use of logarithms , one must pay close attention to the following propositions.
First proposition . In supposing that the logarithm of unity [1] is 0, the logarithm of the product of any two numbers whatever, such as 4 and 8, will always be equal to the sum 5 of the logarithms of the two roots or multiplicands; what is evident for the two progressions cited, is that in adding 2 to 3, one has the sum 5, which is the logarithm of the product 32, which should come effectively; for as 4x8=32, one will have this geometric progression, 1.4::8.32, of which the logarithms should be in an arithmetic proportion, thus one will have 1. l 4: l 8. l 32 (the letter l signifies the logarithm of the number that it precedes); but one knows that in an arithmetic proportion, the sum of the ends is the same as the sum of the middle numbers; thus l 1+ l 32= l 4 + l 8; hence the logarithm of 1 or l 1=0 (by supposition); hence l 32= l 4 + l 8. QED .
Second proposition . The logarithm of quotient 16 of number 64 divided by 4, is equal to the difference there is between the logarithm of 64 and the logarithm of 4; that is to say, l 16= l 64– l 4; for by the supposition 64 ⁄ 16 =16 [2] hence in multiplying by 4, 64x1=16x4, thus 1.4::16.64; therefore l 1+ l 64= l 4+ l 16. As l 1=0, consequently l 64= l 4+ l 16, and so finally l 64– l 4= l 16. QED .
Third proposition . The logarithm of a number is but the half of the logarithm of its square. Demonstration ; take 8, square it, you will have 64. It then remains to prove that l 8= l 64 ⁄ 2 : by the supposition that 8x8=64x1, then 1.8::8.64; thus l 1. l 8: l 8. l 64; then l 1+ l 64= l 8+ l 8=2 l 8, as l 1=0; then l 64=2 l 8, and consequently by dividing each number by 2, one will have l 64 ⁄ 2 l 8. QED .
Fourth proposition . The logarithm of a number is but the third of the logarithm of its cube. Demonstration ; take the number 2, and raise it to its cube 8, I say that l 2= l 8 ⁄ 3 because as 4x2=8x1, one will have 1.2::2.8 hence l 1. l 4: l 2. l 8; therefore, by the preceding demonstration, 4 being the square of 2, l 4=2 l 2; hence l 1. 2 l 2: l 2. l 8; consequently l 1+ l 8= 2 l 2+ l 2= 3 l 2, and as l 1=0, one will have l 8=3 l 2, hence l 8 ⁄ 3 = l 2. QED .
The properties that we have demonstrated have served as the foundations for the construction of tables of logarithms , by means of which one may by addition and subtraction perform the operations that one would, without their assistance, be obliged to carry out by multiplication, division and the extraction of roots, as one will see by going back to the preceding two progressions:
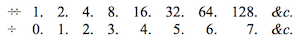
Should you wish to multiply 4 by 16, find the logarithms 2. 4. that correspond to those numbers; sum them to 6, that is the logarithm of their product 64.
Then search in the table for the number that has the logarithm 6, and you will find 64, which is effectively the product of 4 by 16.
If it is a question of dividing 128 by 8, one would find the logarithms 7, 3. From these numbers one would then take 3 away from 7, the result 4 would be the logarithm of their quotient, which corresponds to the number 16.
If one seeks the square root of 64, one has only to take half of its logarithm 6; this is 3 that corresponds to 8, thus 8 is the square root of 64.
It is no more difficult to find the cube root of 64: take the third of its logarithm 6, you will have 2, which corresponds to 4.
Thus 4 is the cube root of 64. One could then carry out with extreme ease the most laborious exercises in calculation if one had the logarithms of a great quantity of numbers; and this is what has been attempted in the construction of tables of logarithms .
The discovery of logarithms is due to Baron Neper, [3] a Scot, who died in 1618. One must however affirm that Stifelius, [4] a German arithmetician, had noted before Napier the fundamental property of logarithms , which is that the logarithm of the product of two numbers is equal to the sum of their logarithms . But this proposition remained fruitless in his hands, and he made no use whatever of it to shorten operations, which was what made Napier’s discovery essential. Kepler [5] also said that Juste Byrge, [6] astronomer of the Landgrave of Hesse, had imagined logarithms , but by the assertion of Kepler himself, the work in which Byrge spoke of them has never appeared.
Napier published his discovery in 1614 in a book entitled mirifici logarithmorum canonis descriptio . The logarithms of numbers that he gives in this work differ from those that we use today in our tables; for in ours the logarithm of 10 is unity, or what is the same thing, 1.000000; and in Napier’s tables, the logarithm of 10 is 2.3025850. We will find under the word Logarithmic the reason for this difference. But this supposition appearing of little use to him, he himself set out tables of logarithms , such as we have today. These were put together after his death by Henry Briggs, in his work titled Arithmetica logarithmica . [7] Adrian Ulacq, mathematician from the Low Countries, perfected the work of Briggs; and since then several others have worked on this topic. The tables of logarithms that today have the best reputation for extent and exactitude are those of Gardiner, in 4º . [8] Those of M. Deparcieux, of the Academy of Sciences, should also be mentioned. [9] See The History of Mathematics by M. Montucla, Vol II Part IV Book I. [10]
Theory of logarithms . Let it be proposed to find the logarithm of any number whatever, and to construct a canon or table for natural logarithms . 1º. As 1, 10, 100, 1000, 10000, etc. constitute a geometric progression, their logarithms can then be taken in an arithmetic progression as desired; hence, to be able to express by decimal fractions the logarithms of all the intermediate numbers, we will take the progression 0.0000000, 1.0000000, 2.0000000, 3.0000000, 4.0000000, etc. in such a manner that the first of these numbers or zero, would be the logarithm of 1, the second would be the logarithm of 10, the third that of 100, and so on as follows. See Decimal. 2º. It is evident that one will not at all find exact logarithms for numbers that are not at all included in the geometric series above, 1, 10, 100, etc. but one will be able to do so by having them come so close to the truth, that in use they will be as good as if they had been exact. To make sense of this, let us suppose that one seeks the logarithm of the number 9; I will introduce between 1.0000000 and 10.0000000 a proportional geometric mean, and searching between the logarithms 0.0000000 and 1.0000000 for a proportional arithmetic mean, this will evidently be the logarithm of the other, that is to say a number that will exceed 3 by a bit more than 1622777 ⁄ 100000000 and consequently will be some distance from 9. I will therefore search between 3 1622777 ⁄ 100000000 and 10 for another proportional geometric mean that will come closer to 9 than the first; and between 10 and this new proportional mean, I will search again for a third, and so on, until I find two consecutive numbers, one of which is just more than, and the other is just less than 9; and by searching for a proportional mean between these two numbers, and then again another between it and that of the two last that will have 9 between it and that before, one will finally arrive at a proportional mean that will be equal to 9 0 ⁄ 1 0000000 ⁄ 0000000 which being no more removed from 9 than by a ten millionth part of unity, its logarithm can, without any detectable error, be taken for the logarithm of 9 itself. I thus come back to my proportional geometric means, and taking one after another, the logarithm of each of them by the introduction of equal proportional arithmetic means, I find in the end that 0.9542425 is the logarithm of the last proportional geometric mean; and I conclude that this number may be taken without detectable error for the logarithm of 9, to which it comes extremely close.
3º. If one finds in the same way the proportional means between 1.0000000 and 3.1622777, which we have seen above to be the proportional mean between 1.0000000 and 10.0000000, and one searches at the same time for the logarithm of each one, one will arrive in the end at a logarithm very close to that of 2, and thus of others. 4º. It is not however necessary to take so much trouble in finding the logarithms of all numbers, for numbers that are the product of two numbers, have as logarithms the sum of the logarithms of their multiplicands; and in reverse, if one has the logarithm of the product of two numbers, and that of one of the multiplicands, one will easily have the logarithm of the other multiplicand; the same, once one has the logarithm of a square, a cube, etc., one thus has that of its root, as was demonstrated in the preceding propositions; consequently, if one takes half the logarithm of 9 derived above, one will have the logarithm of 3, that is 0.4771212.
In logarithms , the numbers that precede the point express whole numbers, and those that are after the point express the numerator of a fraction, of which the denominator is unity, followed
in the same proportion by zeroes as the numerator has figures. One gives these whole numbers the name characteristics , or exponents , because they mark, by adding 1 to them, how many characters there should be for the number to which the logarithm corresponds; thus 0 at the head of a logarithm , or placed in the logarithm ahead of the point, signifies that the corresponding number can have only the character of unities, that is a single figure, because in adding 1 to 0 characteristic, one will have the number 1, which marks the number of figures in the number to which the logarithm corresponds:1 characteristic signifies that the number corresponding to the logarithm , contains not only unities, but also tens, and not hundreds; that in a word, it holds two figures, and that it has its place between ten and one hundred, and so with the other exponents or characteristics. It therefore follows that all numbers, however different they may be, nevertheless have as many characters or figures for the ones as for the others; for example, the numbers between 1 and 10, between 10 and 100, between 100 and 1000, etc. should have logarithms whose characteristic is the same, but which differ by the numbers set to the right of the point.
If the number is only improperly a number, but it is a decimal fraction expressed numerically, which will happen when it has a real character only after the point, then it will evidently have to have a negative logarithm , and furthermore the characteristic of this negative logarithm will mark how many 0 there will be in the number before its first real figure to the left, and including the 0, which is always supposed to be found before the point; thus the logarithm of the decimal fraction 0.256 is 1.40824; that of the decimal fraction 0.0256 is 2.40824, etc.
All this follows from the definition of logarithms ; for as the whole numbers 1, 10, 100, etc. have for logarithms 0, 1, 2, etc. the fractions 1 ⁄ 10 , 1 ⁄ 100 , etc. that form a geometric progression with the whole numbers 1, 10, 100, etc. should have for logarithms the negative numbers 1, 2, etc. that form an arithmetic progression with the numbers 0, 1, 2, etc., then, etc.
Now let it be proposed to find the logarithm of a number that is greater than those found in the tables, but less than 10000000 . Take from the proposed number the first four figures to the left, search in the tables for the logarithm of these four first figures, and add to the characteristic of this logarithm as many unities as remain of the figures to the right in the proposed number. Following this, subtract the found logarithm from that which immediately follows it in the tables, and after this make this proportion, that the difference in the numbers that correspond to these two consecutive logarithms is to the difference in the logarithms themselves, such that what remains to the right in the proposed number is to a fourth term, that we will name the logarithmic difference ; in effect, if you add it to the logarithm already found, you will be able, without detectable error, to take the sum for the logarithm being sought. Were one to seek, for example, the logarithm of the number 92375, I would begin by taking the first four numbers to the left, that is 9237, and I would take from the tables the logar. 3.9655309 of the number that these form by themselves, to which I would add the characteristic 3 [11] of a unity, which would then give me 4.9655309, to which nothing more remains than to add the appropriate logarithmic difference; to determine that, I would take from the tables the logarithm of the number immediately above 9237,
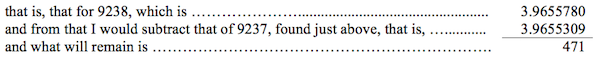
With that set, I would make this proportion: as 10, the difference between 92380 and 92370, is to the difference found just now, that is 471, thus 5 that remains to me to the right in the proposed number, after having removed the first four figures to the left, is the logarithmic difference that I seek, which would consequently be 235;
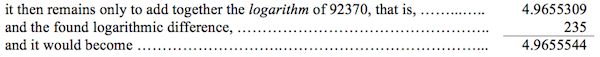
for the value of the logarithm being sought. The reasoning for this operation is that the differences in the three numbers, a , b , c , while these differences are extremely small, are between them, very closely, like the differences in their logarithms . See Logarithmic.
If the proposed number is a fraction or a whole number plus a fraction, one must first reduce the entirety to a fraction, and separately seek the logarithm of the numerator and that of the denominator by the method just given; then one would subtract the two logarithms one from another, and one would have the logarithm of the proposed fraction.
Now let it additionally be proposed to find the number corresponding to a logarithm greater than any that are in the tables . First of all subtract from the given logarithm the logarithm of 10, or that of 100, or that of 1000, or that of 10000, the first in one word, from that type that will give a remainder of a number of characters, such that it will be found in the tables. Find the number corresponding to that remainder considering itself as the logarithm , and multiply the found number by 100, by 1000, or by 10000, etc.; the product will be the number being sought.
Let us suppose, for example, that one seeks the number corresponding to the logarithm 7.7589982, you remove from it the logarithm of the number 10000, which is 4.0000000, and the remainder will be 3.7589982, which corresponds in the tables to the number 5741 11 ⁄ 110 .You then multiply this last number by 1000, and the product 57411100 will be the number being sought. If one proposes to find the number, or to speak more properly, the fraction corresponding to a negative logarithm , it would be necessary to add to the given logarithm the final logarithm in the table, that is, that of the number 10000; or to put it better, it would be necessary to subtract the first taken positively from the second, and to find the number corresponding to the rest of the subtraction regarded as the logarithm . You will make this number the numerator of a fraction, to which you will give 10000 as the denominator, and this fraction will be the number being sought. For example, suppose one seeks the fraction corresponding to the negative logarithm 0.3679767
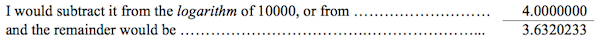
which in the tables corresponds to the number 4285 71 ⁄ 100 so the fraction being sought is therefore 428571 ⁄ 1000000 . One will perceive the reasoning of this rule, in observing that any fraction being the quotient of its numerator by its denominator, unity must be to the fraction as the denominator is to the numerator; but as unity is to the fraction which must correspond to the given negative logarithm , thus 10000 is to the corresponding number to the remainder logarithm ; hence if one takes 10000 for the denominator, and the corresponding number for the numerator, one will have the required fraction.
Let it finally be proposed to find a proportional fourth of three given numbers . You will add the logarithm of the second to that of the third, and from the sum that this addition will have given you, you remove the logarithm of the first, and the remainder will be the logarithm of the fourth number sought. For example, given the numbers 4, 68 and 3,
which should be the logarithm of the number being sought, and as the corresponding number in the tables is 51, I conclude from this that 51 is itself the number being sought.
This problem is used a great deal in Trigonometry. See Triangle and Trigonometry.
All these problems to do with logarithms can evidently be deduced from the theory of logarithms given above; and they can also be demonstrated by the theory of logarithmic, about which one will find its own article.
We will end this by a question that was much debated between Messrs. Leibnitz and Bernoulli. Are the logarithms of negative quantities real, or imaginary? M. Leibnitz held the second, M. Bernoulli held the first. One may see the letters they wrote one another on this subject; they have been printed in the commercium epistolicum of these two great men, published in 1745 in Lausanne. [12] I otherwise had (in 1747 and 1748) a controversy by letters with the celebrated M. Euler on the same subject; he supported the opinion of M. Leibnitz, and I that of M. Bernoulli. This controversy led to a learned memoir by M. Euler, printed in the volume of the academy of Berlin for the year 1709. [13] Since that time, M. de Foncenex has dealt with the same matter in the first volume of the memoirs of the academy of Turin, [14] and declares himself in line with the sentiments of M. Euler, whom he supports with new proofs. I have composed a piece on this subject in which I declare myself to be on the contrary for the opinion of M. Bernoulli. As this piece will probably have seen the light of day before the publication of the present article, I shall not integrate any of it here, and I will content myself with sending my readers to it, as to the pieces of which I have spoken; they will find there all the reasons that one could bring for and against imaginary logarithms of negative quantities. I will limit myself to saying here, 1º. That if one takes between two real and positive numbers, for example 1 and 2, a proportional mean, that proportional mean will be just as good for –√2 as +√2, and that thus the logarithm of –√2 and that of √2 will be the same, that is log 2 ⁄ 2 2º. That if in the equation y = c x and the logarithmic See Logarithmic and Exponential) one makes x = 1 ⁄ 2 y = c½ = ±√ c , and thus the logarithmic will have negative and positive ordinates, in whatever number one will wish to infinity, from which it follows that the logarithms of these ordinates will be the same, that is to say, real quantities. 3º. To these reasons add that which derives from the quadrature of the hyperbole between its asymptotes, of which M. Bernoulli furnished the first, and that I have strengthened with additional proofs; and finally add the many other reasons that one may read in my memoir, along with my responses to Messrs. Euler and de Foncenex, and one will be, I believe, be convinced that the logarithms of negative numbers can be real. I say, can be ; and not are ; this is because in effect one could use systems of logarithms that will render imaginary the logarithms of negative numbers. For example, M. Euler proves very well that if one expresses logarithms by the arcs of imaginary circles, the logarithm of –1 will be imaginary; but at base all systems of logarithms are themselves arbitrary; everything depends on the first supposition one has to make. One says, for example, that the logarithm of unity is = 0, and that the logarithms of fractions are negative. All this is but a supposition; for one could take an arithmetic progression such that the logarithm of unity was not equal to 0, and that logarithms of fractions were real and positive quantities. There is good reason to fear that all this dispute over imaginary logarithms is no more than a dispute over words, and has been so agitated only by a failure of understanding. This is not the first example of a dispute over words in Geometry. See Contingency and Active Force.
Messrs. Gregori, Mercator, Newton, Halley, Cotes, Taylor, etc., have given different methods for the construction of tables of logarithms , that one may see in the Philosophical Transactions . See above all a memoir of M. Halley in the Philosophical Transactions of 1695, nº. 216. [15] Without going into detail here, we will provide a simple enough method for calculating logarithms.
First of all we will suppose ( see the article Logarithmic) that the sub-tangent of the logarithmic is equal to the ordinate that one takes for unity, we will take an ordinate 1– u that would be less than unity, and we will have, in naming the abscissa dx , the equation dx = du ⁄ 1- u as results from the cited article; from which it again follows that x is equal to the logarithm of 1– u , and that the logarithm of 1– u is equal to the integral of - du ⁄ 1- u . Hence, making the division following the ordinary rules, or supposing that 
one finds (see Division , Binomial , Exponent , Series , Suite, etc.) that du ⁄ 1- u = - du - udu - u 2 du - udu , etc. of which the integral is 
, etc., to infiity; and this series is convergent, because the denominators are always diminishing, for u is less than unity. See Fraction. One will then have, in taking a certain number of terms in this succession, the approximate value of the logarithm of 1– u ; hence knowing the logarithm of the fraction 1– u , one will know the logarithm of the number that is the third proportional to this fraction and to unity; for this logarithm is the same, but taken with a positive sign. For example, if one wishes to have the logarithm of the number 10, one will search for that of the fraction 1 ⁄ 10 = 1 9 ⁄ 10 thus u = 19 ⁄ 10 . Then the logarithm of 19 ⁄ 10 is - 9 ⁄ 10 - 81 ⁄ 200 - 729 ⁄ 3000 , etc., and thus as follows; and this quantity taken with the + sign is the logarithm of 10.
All this is true under the hypothesis that the sub-tangent of the logarithm is =1; but were one for example to wish that the logarithm of 10 were 1, in place of being equal to the preceding series, then all the logarithms of the other numbers would need to be multiplied by the ratio of unity to this series. See Logarithmic.
1. In mathematics, the term “unity” is used to refer to the number 1.
2. There is a typographical error in the original text, which has 61 ⁄ 4 = 6, an arithmetical impossibility. I have corrected the translated text.
3. John Napier (1550-1617), Laird of Merchiston in Edinburgh, published Mirifici logarithmorum canonis descriptio: ejusque usus, in utraque trigonometria; ut etiam in omni logistica mathematica, amplissimi, facillimi, & expeditissimi explicatio. Authore ac inventore, Ioanne Nepero, Barone Merchistonii, &c. Scoto. in Edinburgh in 1614. This was published in an English translation in 1616 by Edward Wright, A description of the admirable table oe [ sic ] logarithmes: with a declaration of the most plentiful, easy, and speedy vse thereof in both kindes of trigonometrie, as also in all mathematicall calculations / invented and published in Latin by that honorable L. Iohn Nepair ...; and translated into English by the late learned and famous mathematician Edward Wright ... London: Nicholas Okes.
4. Michael Stifelius (1487-1567) made important contributions to mathematical notation. His Arithmetica integra , published in Nuremberg in 1544, contains a discussion of methods for using addition and subtraction to replace multiplication and division.
5. The German astronomer Johannes Kepler (1571-1630) famously defended Nicolaus Copernicus and the theory of a heliocentric system; Kepler’s Mysterium Cosmographicum was published in Tübingen in 1596.
6. Jost Bürgi (1552-1632) published tables of progressions; see (1620) Aritmetische vnd Geometrische Progress Tabulen, sambt gründlichem vnterricht, wie solche nützlich in allerley Rechnungen zugebrauchen, vnd verstanden werden sol . Prague: University of Prague.
7. Henry Briggs (1561-1630) published Arithmetica Logarithmica, sicve Logarithmorum Chiliades Triginta, pro numeris naturali serie crescentibus ... in London in 1624.
8. William Gardiner (1717) London: R. and W. Mount, and T. Page, in Paternoster-Row.
9. Antoine Deparcieux (1741) Nouveaux traites de trigonometrie rectiligne et spherique. Demontres par une Methode nouvelle & plus facile que celle que l’on a employe jusqu’a present ... Paris: Chez Hippolyte-Louis Guerin & Jacques Guerin, libraires, rue saint Jacques, à Saint Thomas d’Aquin.
10. Jean-Etienne Montucla (1758) Histoire des mathematiques dans laquelle on rend compte de leurs progres depuis leur origine jusqu’a nos jours ... [Vol II] Paris: Chez Ch. Ant. Jombert, Imprimeur-Libraire du Roi pour l’Artillerie & la Génie, rue Dauphine, à l’Image Notre-Dame.
11. This appears to be a typographical error; context (and the preceding arguments) would imply adding “1” here instead of “3”.
12. Commercium philosophicum et mathematicum. Ab anno 1694. ad annum 1716 . Lausanne & Geneva (1745), Marci Michaelis Bousquet.
13. This date is incorrect because Leonhard Euler was born in 1707 and died in 1783. The mentioned article appears to be “De la controverse entre Mrs. Leibniz et Bernoulli sur les logarithmes des nombres negatifs et imaginaires”, Histoire de l’Académie des Sciences et des Belles-Lettres de Berlin , Volume 5, pages 139-179, dated 1749 and issued in 1751.
14. François Daviet de Foncenex (1754) “Reflexions sur les quantités imaginaires”, Miscellanea Philosophico-Mathematica Societatis Privatae Taurinensis, Tomus Primus, 113-146.
15. Edmond Halley (1695) “A Most Compendious and Facile Method for Constructing the Logarithms, Exemplified and Demonstrated from the Nature of Numbers, without any Regard to the Hyperbola, with a Speedy Method for Finding the Number from the Logarithm Given. By E. Halley.” Philosophical Transactions 1695-1697, volume 19, pages 58-67.

