| Title: | Combination |
| Original Title: | Combinaison |
| Volume and Page: | Vol. 3 (1753), pp. 663–664 |
| Author: | Jean-Baptiste le Rond d'Alembert (biography) |
| Translator: | Richard J. Pulskamp [Xavier University] |
| Subject terms: |
Mathematics
|
| Original Version (ARTFL): | Link |
| Source: | Originally published at http://www.cs.xu.edu/math/Sources/Dalembert/ ; used by permission |
| Rights/Permissions: |
This text is protected by copyright and may be linked to without seeking permission. Please see http://quod.lib.umich.edu/d/did/terms.html for information on reproduction. |
| URL: | http://hdl.handle.net/2027/spo.did2222.0001.117 |
| Citation (MLA): | d'Alembert, Jean-Baptiste le Rond. "Combination." The Encyclopedia of Diderot & d'Alembert Collaborative Translation Project. Translated by Richard J. Pulskamp. Ann Arbor: Michigan Publishing, University of Michigan Library, 2009. Web. [fill in today's date in the form 18 Apr. 2009 and remove square brackets]. <http://hdl.handle.net/2027/spo.did2222.0001.117>. Trans. of "Combinaison," Encyclopédie ou Dictionnaire raisonné des sciences, des arts et des métiers, vol. 3. Paris, 1753. |
| Citation (Chicago): | d'Alembert, Jean-Baptiste le Rond. "Combination." The Encyclopedia of Diderot & d'Alembert Collaborative Translation Project. Translated by Richard J. Pulskamp. Ann Arbor: Michigan Publishing, University of Michigan Library, 2009. http://hdl.handle.net/2027/spo.did2222.0001.117 (accessed [fill in today's date in the form April 18, 2009 and remove square brackets]). Originally published as "Combinaison," Encyclopédie ou Dictionnaire raisonné des sciences, des arts et des métiers, 3:663–664 (Paris, 1753). |
Combination should be said properly only of the collection of many things two by two; but one applies it in mathematics to all the possible ways of taking a number of given quantities.
Father Mersenne has given the combinations of all the notes and sounds of Music to the number 64; the sum which comes of it is able to be expressed, according to him, only with 60 digits or figures.
Father Sébastien has shown in the Mémoires de l'Academie 1704, that two tiles split each by their diagonals into two triangles of different colors, provide 64 different arrangements of the chessboard: that which must astonish, when one considers that two figures would know to combine themselves only in two ways. See, Franc-Carreau.
One can make use of this remark by Father Sébastien, in order to tile some apartments.
Doctrine of combinations . A number of quantities being given with the one of the quantities which must enter into each combination , to find the number of combinations .
A single quantity, as it is evident, does not admit of combination ; two quantities a and b give one combination ; three quantities a, b, c, combined two by two, give three combinations ab, ac, bc; four of them would give six ab, ac, bc, ad, bd, cd ; five of them would give ten ab, ac, bc, ad, bd, cd, ae, be, ce, de.
In general the sequence of the numbers of combinations is 1, 3, 6, 10, etc. that is to say the sequence of triangular numbers; thus q representing the number of the quantities to combine, 
will
be the number of their
combinations two by two.
See Triangular numbers.
If one has three quantities a, b,
c to combine three by three, they will provide only a
single
combination abc; if
one takes a fourth quantity
d , the
combinations that these
four quantities are able to have
three by three, will be the four abc,
abd, bcd, acd; if one takes
a fifth of them, one will have ten
combinations abc, abd, bcd, acd, abe,
bde, bce, ace,
ade ; [1]
if one takes a sixth of them, one will have twenty , etc. So that
the sequence of
combinations three by
three is that of the pyramidal numbers; and as
q
expressing always the number of given quantities,
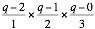
, is the one of
their combinations three by
three.
The number of combinations four by four of the same quantities would be
found in the same manner

; and in general
n expressing the number of
letters which one
wishes to introduce into each term of the combination, the quantity 
will express the demanded number of combinations .
If one demands, for example, in how many ways are six quantities are able
to be taken four by four, one will
put q = 6 and
n = 4, and one will
substitute these numbers into the
preceding formula, that which will give 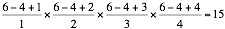
.
Corollary . If one wishes to have all the possible combinations of any number of letters, taken so many two by two as three by three, as 4 by 4, etc. it will be necessary to add all the preceding formulas
; etc. that is to say that the number of all these combinations will be expressed by
etc.
If one compares presently this sequence with that which represents the raising of any binomial to the power q , one will see that by making equal to unity each of the terms of this binomial, the two sequences are the same at the two first terms near 1, and q , which is lacking in the preceding sequence. From there it follows that instead of this sequence, one can write 2q – 1 – q this which give a very simple way to have all the possible combinations from a number q of letters. Let this number be, for example 5, one will have therefore for the total number of its combinations 25 – 5 – 1 = 32 – 6 = 26. See Binomial.
Any number of quantities being given, to find the number of combinations and of alternations which they are able to receive, by taking them in all possible ways.
We suppose first that there are only two quantities a , b one will have first ab and ba , that is to say the number 2; and as each of these quantities can also be combined with itself, one will have again aa and bb , that is to say that the number of combinations and alternations is in this case 2 + 2 = 4. If there are three quantities a, b, c, and if the exponent of their variation be two, one will have three terms for their combinations , which are ab, bc, ac : to these three terms one will add again three others ba, cb, ca, for the alternations; and finally three others for the combinations aa, bb, cc, of the letters a, b, c, taken each with itself, this which will give 3 + 3 + 3 = 9. In general it will be easy to see that if the number of the quantities is n , and if the exponent of the variation be 2, n2 will be the one of all their combinations and of their alternations.
If the exponent of the variation is 3, and if one supposes first only three letters a, b, c, one will have for all the combinations and alternations aaa, aab, aba, baa, abb, aac, aca, caa, abc, bac, bca, acb, cab, cba, acc, cac, cca, bba, bab, bbb, bbc, cbb, bcb, bcc, cbc, ccb, ccc, that is to say the number 27 or 3 3 .
In the same way, if the number of letters were 4, the exponent of the variation 3, 4 3 or 64, would be the number of combinations and alternations. And in general if the number of the letters were n, n 3 would be the one of the combinations and alternations for the exponent 3. Finally if the exponent is any number, m, n m will express all the combinations and alternations for this exponent.
If one wishes therefore all the combinations and alternations of a number n of letters in all the possible varieties, it will be necessary to sum the series n n + n n-1 + n n-2 + n n-3 + n n-4 + n n-5 + n n-6 etc. until the last term which is n .
Now as all the terms of this sequence are in geometric progression, and as one has the first term n n , the second n n-1 , and the last n , it follows that one will have also the sum of this progression, which will be

.
Let n , for example, be equal to 4, the number of all the possible combinations and alternations will be
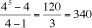
. Let n be 24, one will have then for all the possible combinations and alternations
; and it is this enormous number which expresses the combinations of all the letters of the alphabet among themselves.See the Ars Conjectandi of Jacques Bernoulli, and L'Analyse des jeux de hasard of Montmort. These two authors, especially the first, have treated with great care the matter of combinations. This theory is in fact very useful in the calculus of the games of chance; and it is on it that ride all the science of probabilities. See Game, Wager, Advantage, Probability, Certitude, etc.
It is clear that the science of anagrams (see Anagramme) depends on that of combinations. For example, in Roma which is composed of four letters, there are twenty- four combinations (see Permutation); and of these twenty-four combinations one will find many which form Latin words, armo, ramo, mora, amor, maro; one finds also omar ; likewise in Rome, one finds more, omer, etc.
Note
1. The combination is omitted.


