| Title: | Heads or Tails |
| Original Title: | Croix ou pile |
| Volume and Page: | Vol. 4 (1754), pp. 512–513 |
| Author: | Jean-Baptiste le Rond d'Alembert (biography) |
| Translator: | Jeff Suzuki |
| Subject terms: |
Calculus of probabilities
|
| Original Version (ARTFL): | Link |
| Rights/Permissions: |
This text is protected by copyright and may be linked to without seeking permission. Please see http://quod.lib.umich.edu/d/did/terms.html for information on reproduction. |
| URL: | http://hdl.handle.net/2027/spo.did2222.0000.122 |
| Citation (MLA): | d'Alembert, Jean-Baptiste le Rond. "Heads or Tails." The Encyclopedia of Diderot & d'Alembert Collaborative Translation Project. Translated by Jeff Suzuki. Ann Arbor: Michigan Publishing, University of Michigan Library, 2003. Web. [fill in today's date in the form 18 Apr. 2009 and remove square brackets]. <http://hdl.handle.net/2027/spo.did2222.0000.122>. Trans. of "Croix ou pile," Encyclopédie ou Dictionnaire raisonné des sciences, des arts et des métiers, vol. 4. Paris, 1754. |
| Citation (Chicago): | d'Alembert, Jean-Baptiste le Rond. "Heads or Tails." The Encyclopedia of Diderot & d'Alembert Collaborative Translation Project. Translated by Jeff Suzuki. Ann Arbor: Michigan Publishing, University of Michigan Library, 2003. http://hdl.handle.net/2027/spo.did2222.0000.122 (accessed [fill in today's date in the form April 18, 2009 and remove square brackets]). Originally published as "Croix ou pile," Encyclopédie ou Dictionnaire raisonné des sciences, des arts et des métiers, 4:512–513 (Paris, 1754). |
Cross or tails ( analysis of chance ). This well-known game, which has no need for explanation, will supply us with the following observations. One asks what is the chance of obtaining a cross in two consecutive throws. The answer that one finds elsewhere, and following the ordinary principles, is this: There are four combinations,
| First Toss. | Second Toss. |
| Cross. | Cross. |
| Tails. | Cross. |
| Cross. | Tails. |
| Tails. | Tails. |
Of these four combinations one results in a loss, and three make a win; the odds are thus 3 against to 1 in favor of the player who throws the piece. If there were three throws, one has eight combinations of which a single one causes a loss, and seven make a win; thus there are 7 against to 1 in favor. See Combinations and Advantage. However, is this correct? Because if we take the case of two throws, is it not necessary [p. 513] to reduce to two combinations which give cross on the first throw? Because if cross appears on the first throw, the game is finished, and the second throw counts for nothing. Thus there are properly only three possible combinations:
Cross , first throw. Tails , cross , first and second throw. Tails , tails , first and second throw. Thus there are only 2 against to 1 in favor. Likewise in the case of three throws, one finds
Cross . Tails , cross . Tails , tails , cross . Tails , tails , tails . Thus there are only 3 against to 1 in favor: this is worthy, it seems to me, of the attention of the Calculators, and of the need to reform many of the unanimously accepted rules of games of chance.
Another question. Pierre plays against Paul on the condition, that if Pierre obtains cross on the first throw, he will pay one ecu to Paul; if he only obtains cross on the second throw, two ecus; if on the third throw, four, and so on. One finds by the ordinary rules (following the principles that we have just supposed), that the expectation of Paul, and consequently that which he should wager for this game 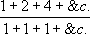
a quantity which is found to be infinite. However there is no person who would want to wager for this game a sum nearly as large. One can see in the mémoires de l'académie de Petersbourg, Vol. V ., some attempts to resolve this difficulty; but we do not know if these will prove satisfactory; and there is here some scandal which well deserves the attention of the Algebraists. What appears surprising in the solution to this problem, is the infinite quantity that one finds for the expectation of Paul. But one notes that the expectation of Paul needs to be equal to the risk of Pierre. Thus it is only a question of finding if the risk of Pierre is infinite, that is to say (follow the true notion of the infinite) if this risk is can be supposed greater than any fixed finite number. However, if one thinks a little on the question, one sees that this risk is that in effect. Because this risk increases with the number of throws, which is very evident by the computation. Now the number of throws can become and will be in effect infinite, since by the conditions of the game the number is not fixed. Thus the indefinite number of throws is one of the reasons which here makes the risk to Pierre infinite. See Absent and Probability.
According to a very knowledgeable geometer with whom I discussed this matter one day, the expectation of Paul and his stakes can never be infinite, because that of Pierre cannot be; and that if Pierre has, for example, only 2 20 ecus, he ought only to make 21 throws, after which he should stop, because Pierre will not be in a position to pay. Thus the number of possible throws is determinate, finite, and equal to 21, and one finds that the expectation of Paul is. 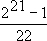
Although this sum is no longer infinite, I doubt that any player would want to wager it. Thus this solution, however ingenious that it is, does not initially appear to resolve this difficulty. However all things being carefully examined, it seems to me that one must be satisfied with it. Because it is not a question here of the difficulty or ease with which Paul will risk the sum in question, it is only a question of what he needs to wager to play the game equitably with Pierre; and it is certain that this amount will be given by the sum above. Paul would without a doubt be a fool to wager, but he would not be alone, because Pierre is also foolish to propose a game whereby Pierre could lose in a minute an immense sum to him. But, for a foolish player to game equitably, he needs to find a fool like himself. If Pierre played a single time, wagering a million if he obtained tails, he should wager for each play a half-million: this is incontestable. However there are only two fools who could play an equitable game.
We note that for this occasion, that to make more complete, and thus to say more than usual, the solutions to the problems concerning games, it is desirable to enter into moral considerations, relative to the fortunes of the players, to their profession, situation, their strengths (when it is a question of games of commerce), and so on. It is certain, for example, that for two men unequally wealthy who play an equitable game following the ordinary rules, the one who is less wealthy risks more than the other. But since all these considerations are nearly impossible to subject to computation because of the variety of circumstances, one is obliged to make abstraction of them, and resolve the problem mathematically, and suppose moreover the moral circumstances are perfectly equal between one and the other, or neglect them completely. These are the circumstances, when one brought to one's attention, that lead one to believe the computation is defective, when they are not. See Advantage, Game, Wager, &c.
