Mathematical tracts on the lunar and planetary theories, the figure of the earth, precession and nutation, the calculus of variations, and the undulatory theory of optics.
Annotations Tools
262 UNDULATORY TIEORY OP OPTICS. Case 1. Suppose X much greater than b. (This will generally be the case with sound, as for all audible sounds X varies from a few inches to several feet.) Here - O will be a small arc, and will not differ X much from its sine: putting the arc for the sine, the maximum of vibration becomes cX 2 7rb cos 0 2cb, or -,5 7rrcosO r which is the same for all values of 0. Case 2. Suppose X much smaller than b. (This will generally be the case with light.) For the part nearly opposite to the entering wave, cos 0 is very small, and cX 27rb cos 2cb.sin - 7r cos 0 \X r In other parts it is to be observed that the disturbance is o when 27rb cos 0 - r or =o 2r, or = 2, or = 7r, &c., that is, when X 2X 3X cos O= 6 -, or =5 or = - &c. 2b 2b 2b Hence there is a succession of points in which there is absolute darkness. Of the intermediate parts, the brightest will be found (nearly) by making 27b cos 0 sin = 1 cX then the maximum of vibration is.Consequently -r cos the intensity of light at the brightest part of one of the bright portions is to that of the part nearly opposite to the entering
-
Scan #1

Page #1
-
Scan #2

Page #2
-
Scan #3

Page #3
-
Scan #4

Page #4
-
Scan #5

Page #5
-
Scan #6

Page #6 - Title Page
-
Scan #7

Page #7
-
Scan #8

Page #8 - Title Page
-
Scan #9

Page #9
-
Scan #10

Page V
-
Scan #11

Page VI
-
Scan #12

Page VII
-
Scan #13

Page VIII
-
Scan #14

Page 1
-
Scan #15

Page 2
-
Scan #16

Page 3
-
Scan #17

Page 4
-
Scan #18

Page 5
-
Scan #19

Page 6
-
Scan #20

Page 7
-
Scan #21

Page 8
-
Scan #22

Page 9
-
Scan #23

Page 10
-
Scan #24

Page 11
-
Scan #25

Page 12
-
Scan #26

Page 13
-
Scan #27

Page 14
-
Scan #28

Page 15
-
Scan #29

Page 16
-
Scan #30

Page 17
-
Scan #31

Page 18
-
Scan #32

Page 19
-
Scan #33

Page 20
-
Scan #34
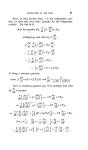
Page 21
-
Scan #35
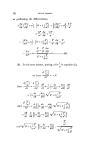
Page 22
-
Scan #36

Page 23
-
Scan #37
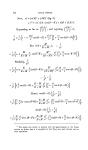
Page 24
-
Scan #38

Page 25
-
Scan #39

Page 26
-
Scan #40

Page 27
-
Scan #41

Page 28
-
Scan #42

Page 29
-
Scan #43

Page 30
-
Scan #44

Page 31
-
Scan #45

Page 32
-
Scan #46

Page 33
-
Scan #47

Page 34
-
Scan #48

Page 35
-
Scan #49

Page 36
-
Scan #50

Page 37
-
Scan #51

Page 38
-
Scan #52

Page 39
-
Scan #53

Page 40
-
Scan #54

Page 41
-
Scan #55

Page 42
-
Scan #56

Page 43
-
Scan #57

Page 44
-
Scan #58

Page 45
-
Scan #59

Page 46
-
Scan #60

Page 47
-
Scan #61

Page 48
-
Scan #62

Page 49
-
Scan #63

Page 50
-
Scan #64

Page 51
-
Scan #65

Page 52
-
Scan #66

Page 53
-
Scan #67

Page 54
-
Scan #68

Page 55
-
Scan #69

Page 56
-
Scan #70

Page 57
-
Scan #71

Page 58
-
Scan #72

Page 59
-
Scan #73

Page 60
-
Scan #74

Page 61
-
Scan #75

Page 62
-
Scan #76

Page 63
-
Scan #77

Page 64
-
Scan #78

Page 65
-
Scan #79

Page 66
-
Scan #80

Page 67
-
Scan #81

Page 68
-
Scan #82

Page 69
-
Scan #83

Page 70
-
Scan #84

Page 71
-
Scan #85

Page 72
-
Scan #86

Page 73
-
Scan #87

Page 74
-
Scan #88

Page 75
-
Scan #89

Page 76
-
Scan #90

Page 77
-
Scan #91

Page 78
-
Scan #92

Page 79
-
Scan #93

Page 80
-
Scan #94

Page 81
-
Scan #95

Page 82
-
Scan #96

Page 83
-
Scan #97

Page 84
-
Scan #98

Page 85
-
Scan #99

Page 86
-
Scan #100

Page 87
-
Scan #101

Page 88
-
Scan #102

Page 89
-
Scan #103

Page 90
-
Scan #104

Page 91
-
Scan #105

Page 92
-
Scan #106

Page 93
-
Scan #107

Page 94
-
Scan #108

Page 95
-
Scan #109

Page 96
-
Scan #110

Page 97
-
Scan #111

Page 98
-
Scan #112

Page 99
-
Scan #113

Page 100
-
Scan #114

Page 101
-
Scan #115

Page 102
-
Scan #116

Page 103
-
Scan #117

Page 104
-
Scan #118

Page 105
-
Scan #119

Page 106
-
Scan #120

Page 107
-
Scan #121

Page 108
-
Scan #122

Page 109
-
Scan #123

Page 110
-
Scan #124

Page 111
-
Scan #125

Page 112
-
Scan #126

Page 113
-
Scan #127

Page 114
-
Scan #128

Page 115
-
Scan #129

Page 116
-
Scan #130

Page 117
-
Scan #131

Page 118
-
Scan #132

Page 119
-
Scan #133

Page 120
-
Scan #134

Page 121
-
Scan #135

Page 122
-
Scan #136

Page 123
-
Scan #137

Page 124
-
Scan #138

Page 125
-
Scan #139

Page 126
-
Scan #140

Page 127
-
Scan #141

Page 128
-
Scan #142

Page 129
-
Scan #143
Page 130
-
Scan #144

Page 131
-
Scan #145

Page 132
-
Scan #146

Page 133
-
Scan #147

Page 134
-
Scan #148

Page 135
-
Scan #149

Page 136
-
Scan #150

Page 137
-
Scan #151

Page 138
-
Scan #152

Page 139
-
Scan #153

Page 140
-
Scan #154

Page 141
-
Scan #155

Page 142
-
Scan #156

Page 143
-
Scan #157

Page 144
-
Scan #158

Page 145
-
Scan #159

Page 146
-
Scan #160

Page 147
-
Scan #161

Page 148
-
Scan #162

Page 149
-
Scan #163

Page 150
-
Scan #164

Page 151
-
Scan #165

Page 152
-
Scan #166

Page 153
-
Scan #167

Page 154
-
Scan #168

Page 155
-
Scan #169

Page 156
-
Scan #170

Page 157
-
Scan #171

Page 158
-
Scan #172

Page 159
-
Scan #173

Page 160
-
Scan #174

Page 161
-
Scan #175

Page 162
-
Scan #176

Page 163
-
Scan #177

Page 164
-
Scan #178

Page 165
-
Scan #179

Page 166
-
Scan #180

Page 167
-
Scan #181

Page 168
-
Scan #182

Page 169
-
Scan #183

Page 170
-
Scan #184

Page 171
-
Scan #185

Page 172
-
Scan #186

Page 173
-
Scan #187

Page 174
-
Scan #188

Page 175
-
Scan #189

Page 176
-
Scan #190

Page 177
-
Scan #191

Page 178
-
Scan #192

Page 179
-
Scan #193

Page 180
-
Scan #194

Page 181
-
Scan #195

Page 182
-
Scan #196

Page 183
-
Scan #197

Page 184
-
Scan #198

Page 185
-
Scan #199

Page 186
-
Scan #200

Page 187
-
Scan #201

Page 188
-
Scan #202

Page 189
-
Scan #203

Page 190
-
Scan #204

Page 191
-
Scan #205

Page 192
-
Scan #206

Page 193
-
Scan #207

Page 194
-
Scan #208

Page 195
-
Scan #209

Page 196
-
Scan #210

Page 197
-
Scan #211

Page 198
-
Scan #212

Page 199
-
Scan #213

Page 200
-
Scan #214

Page 201
-
Scan #215

Page 202
-
Scan #216

Page 203
-
Scan #217

Page 204
-
Scan #218

Page 205
-
Scan #219

Page 206
-
Scan #220

Page 207
-
Scan #221

Page 208
-
Scan #222

Page 209
-
Scan #223

Page 210
-
Scan #224

Page 211
-
Scan #225

Page 212
-
Scan #226

Page 213
-
Scan #227

Page 214
-
Scan #228

Page 215
-
Scan #229

Page 216
-
Scan #230

Page 217
-
Scan #231

Page 218
-
Scan #232

Page 219
-
Scan #233

Page 220
-
Scan #234

Page 221
-
Scan #235

Page 222
-
Scan #236

Page 223
-
Scan #237

Page 224
-
Scan #238

Page 225
-
Scan #239

Page 226
-
Scan #240

Page 227
-
Scan #241

Page 228
-
Scan #242

Page 229
-
Scan #243

Page 230
-
Scan #244

Page 231
-
Scan #245

Page 232
-
Scan #246

Page 233
-
Scan #247

Page 234
-
Scan #248

Page 235
-
Scan #249

Page 236
-
Scan #250

Page 237
-
Scan #251

Page 238
-
Scan #252

Page 239
-
Scan #253

Page 240
-
Scan #254

Page 241
-
Scan #255

Page 242
-
Scan #256

Page 243
-
Scan #257

Page 244
-
Scan #258

Page 245
-
Scan #259

Page 246
-
Scan #260

Page 247
-
Scan #261

Page 248
-
Scan #262

Page 249
-
Scan #263

Page 250
-
Scan #264

Page 251
-
Scan #265

Page 252
-
Scan #266

Page 253
-
Scan #267

Page 254
-
Scan #268

Page 255
-
Scan #269

Page 256
-
Scan #270

Page 257
-
Scan #271

Page 258
-
Scan #272

Page 259
-
Scan #273

Page 260
-
Scan #274

Page 261
-
Scan #275

Page 262
-
Scan #276

Page 263
-
Scan #277

Page 264
-
Scan #278

Page 265
-
Scan #279

Page 266
-
Scan #280

Page 267
-
Scan #281

Page 268
-
Scan #282

Page 269
-
Scan #283

Page 270
-
Scan #284

Page 271
-
Scan #285

Page 272
-
Scan #286

Page 273
-
Scan #287

Page 274
-
Scan #288

Page 275
-
Scan #289

Page 276
-
Scan #290

Page 277
-
Scan #291

Page 278
-
Scan #292

Page 279
-
Scan #293

Page 280
-
Scan #294

Page 281
-
Scan #295

Page 282
-
Scan #296

Page 283
-
Scan #297

Page 284
-
Scan #298

Page 285
-
Scan #299

Page 286
-
Scan #300

Page 287
-
Scan #301

Page 288
-
Scan #302

Page 289
-
Scan #303

Page 290
-
Scan #304

Page 291
-
Scan #305

Page 292
-
Scan #306

Page 293
-
Scan #307

Page 294
-
Scan #308

Page 295
-
Scan #309

Page 296
-
Scan #310

Page 297
-
Scan #311

Page 298
-
Scan #312

Page 299
-
Scan #313

Page 300
-
Scan #314

Page 301
-
Scan #315

Page 302
-
Scan #316

Page 303
-
Scan #317

Page 304
-
Scan #318

Page 305
-
Scan #319

Page 306
-
Scan #320

Page 307
-
Scan #321

Page 308
-
Scan #322

Page 309
-
Scan #323

Page 310
-
Scan #324

Page 311
-
Scan #325

Page 312
-
Scan #326

Page 313
-
Scan #327

Page 314
-
Scan #328

Page 315
-
Scan #329

Page 316
-
Scan #330

Page 317
-
Scan #331

Page 318
-
Scan #332

Page 319
-
Scan #333

Page 320
-
Scan #334

Page 321
-
Scan #335

Page 322
-
Scan #336

Page 323
-
Scan #337

Page 324
-
Scan #338

Page 325
-
Scan #339

Page 326
-
Scan #340

Page 327
-
Scan #341

Page 328
-
Scan #342

Page 329
-
Scan #343

Page 330
-
Scan #344

Page 331
-
Scan #345

Page 332
-
Scan #346

Page 333
-
Scan #347

Page 334
-
Scan #348

Page 335
-
Scan #349

Page 336
-
Scan #350

Page 337
-
Scan #351

Page 338
-
Scan #352

Page 339
-
Scan #353

Page 340
-
Scan #354

Page 341
-
Scan #355

Page 342
-
Scan #356

Page 343
-
Scan #357

Page 344
-
Scan #358

Page 345
-
Scan #359

Page 346
-
Scan #360

Page 347
-
Scan #361

Page 348
-
Scan #362

Page 349
-
Scan #363

Page 350
-
Scan #364

Page 351
-
Scan #365

Page 352
-
Scan #366

Page 353
-
Scan #367

Page 354
-
Scan #368

Page 355
-
Scan #369

Page 356
-
Scan #370

Page 357
-
Scan #371

Page 358
-
Scan #372

Page 359
-
Scan #373

Page 360
-
Scan #374

Page 361
-
Scan #375

Page 362
-
Scan #376

Page 363
-
Scan #377

Page 364
-
Scan #378

Page 365
-
Scan #379

Page 366
-
Scan #380

Page 367
-
Scan #381

Page 368
-
Scan #382

Page 369
-
Scan #383

Page 370
-
Scan #384

Page 371
-
Scan #385

Page 372
-
Scan #386

Page 373
-
Scan #387

Page 374
-
Scan #388

Page 375
-
Scan #389

Page 376
-
Scan #390

Page 377
-
Scan #391

Page 378
-
Scan #392

Page 379
-
Scan #393

Page 380
-
Scan #394

Page 381
-
Scan #395

Page 382
-
Scan #396

Page 383
-
Scan #397

Page 384
-
Scan #398

Page 385
-
Scan #399

Page 386
-
Scan #400

Page 387
-
Scan #401

Page 388
-
Scan #402

Page 389
-
Scan #403

Page 390
-
Scan #404

Page 1
-
Scan #405

Page #405
-
Scan #406

Page 2
-
Scan #407

Page #407
-
Scan #408
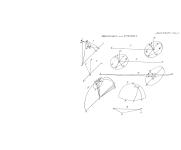
Page 3
-
Scan #409

Page #409
-
Scan #410

Page 4
-
Scan #411

Page #411
-
Scan #412

Page 5
-
Scan #413

Page #413
-
Scan #414

Page #414
-
Scan #415

Page #415
Actions
About this Item
- Title
- Mathematical tracts on the lunar and planetary theories, the figure of the earth, precession and nutation, the calculus of variations, and the undulatory theory of optics.
- Author
- Airy, George Biddell, Sir, 1801-1892.
- Canvas
- Page 248
- Publication
- Cambridge,: J. & J.J. Deighton;
- 1842.
- Subject terms
- Celestial mechanics.
- Calculus of variations
- Geometrical optics.
Technical Details
- Link to this Item
-
https://name.umdl.umich.edu/aan8938.0001.001
- Link to this scan
-
https://quod.lib.umich.edu/u/umhistmath/aan8938.0001.001/275
Rights and Permissions
The University of Michigan Library provides access to these materials for educational and research purposes. These materials are in the public domain in the United States. If you have questions about the collection, please contact Historical Mathematics Digital Collection Help at [email protected]. If you have concerns about the inclusion of an item in this collection, please contact Library Information Technology at [email protected].
DPLA Rights Statement: No Copyright - United States
Related Links
IIIF
- Manifest
-
https://quod.lib.umich.edu/cgi/t/text/api/manifest/umhistmath:aan8938.0001.001
Cite this Item
- Full citation
-
"Mathematical tracts on the lunar and planetary theories, the figure of the earth, precession and nutation, the calculus of variations, and the undulatory theory of optics." In the digital collection University of Michigan Historical Math Collection. https://name.umdl.umich.edu/aan8938.0001.001. University of Michigan Library Digital Collections. Accessed April 30, 2025.