Elements of descriptive geometry, with applications to isometric projection and othe forms of one-plane projection; a text-book for colleges and ingineering schools by O. E. Randall.

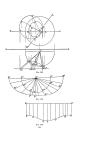
ISOMETRIC PROJECTION

195

measured upon either one of these axes is 1 foot times the natural
cosine of 35~.16', which is equal to.81647 ft.
If this length is divided into twelve equal parts, each one of
these divisions will represent the isometric projection of an inch
measured under the conditions mentioned above. In the same
way we may subdivide the inch and thus establish an isometric
scale by which we may determine the length in isometric projection of any distance measured upon the coordinate axes or upon
any lines parallel to these axes.
Since drawings are usually made either on a smaller or a larger
scale than the object represented, and since on account of the equal
inclination of the coordinate axes to the plane of projection, the projections of distances measured along these lines are equally foreshortened, there is no good reason why any other than the ordinary
foot scale should be used in connection with this form of projection.
The isometric scale is therefore not used in practical drafting.
431. Shade Lines. In isometric projection the rays of light are
assumed parallel to the plane of projection and inclined at an
angle of 30 degrees with the horizon. With these exceptions,
shade lines in isometric projection are determined and represented
precisely as in orthographic projection.
If the cube to whose diagonal rays of light in orthographic projection have been referred (see Section 230) is so placed that the
diagonal passing through the upper right-hand front vertex of the
cube is perpendicular to V, and so that the right-hand vertical edge
of the cube is still in a vertical plane, the diagonal passing through
the upper left-hand front vertex of the cube in its first position -
the diagonal to which rays of light in orthographic projection
were referred - will in the new position be parallel to V and make
an angle of 30 degrees with H.
In isometric projection, then, rays of light may be referred to the
same diagonal of the cube as in orthographic projection, provided
the cube occupies the position indicated above.
432. General Instructions in regard to Solution of Problems.
The isometric projection of a point whose coordinates with reference to two coordinate axes are known is the intersection of the
isometric projections of the two coordinate lines of the point.