An introduction to projective geometry and its applications; an analytic and synthetic treatment, by Arnold Emch ...
Annotations Tools
266 INDEX. PAGE Projective properties of the circle.................................. 35 ranges and pencils.................................. 5 5, 30 theorems, statical proofs of.............................. 220 transformations of the plane............................. 59 transformations of the points of a straight line.............. 5 Quadrilateral.................................................... 26 Quadruple, Steinerian........................................... 203 Rabattem ent................................................... 77 Realization of collineations by linkages............................. 242 Reciprocal polars.......................................... 123 Reciprocal transformation...................................... I23, I26 Rectangular pair of an involution................................... 9 Reye...................................................... 5, 6, 92 Reve's configuration.................................. 86 R itter, H....................................................... 257 R itter, W.................................................. 228, 229 R oberts......................................................... 242 R otation........................................................ 59 Rotation., 59 R otator......................................................... 251 Salm on....................................................... 25, I35 Scheiner's pantograph........................................... 250 Self-polar triangle............................................. 42, I03 Sim ilitude....................................................... 52 Special cases of central projection.................................. 51 Special constructions of conics by central projection and parallel projection 146 Statical proofs or some projective theorems......................... 220 Steiner..................................... 5, 22, 92, 85, 203 Steinerian quadruple......................................... 203 Steinerian transformation.......................................... 85 Steiner's theorem................................................ I37 Stress ellipse.................................................... 229 Stresses in a plane..................................... 223 Sylvester........................................................ 242 Sylvester's pantograph........................................... 249 Symmetry....................................................... 56 Tangent and polar............................................... 8 Tangents from a point to a conic.................................. 163 T aylor.......................................................... 45
-
Scan #1

Page #1
-
Scan #2

Page #2
-
Scan #3

Page #3
-
Scan #4

Page #4 - Title Page
-
Scan #5

Page #5
-
Scan #6

Page III
-
Scan #7

Page IV
-
Scan #8

Page V - Table of Contents
-
Scan #9

Page VI - Table of Contents
-
Scan #10

Page VII - Table of Contents
-
Scan #11

Page #11
-
Scan #12

Page 1
-
Scan #13

Page 2
-
Scan #14

Page 3
-
Scan #15

Page 4
-
Scan #16

Page 5
-
Scan #17

Page 6
-
Scan #18

Page 7
-
Scan #19

Page 8
-
Scan #20

Page 9
-
Scan #21

Page 10
-
Scan #22

Page 11
-
Scan #23

Page 12
-
Scan #24

Page 13
-
Scan #25

Page 14
-
Scan #26

Page 15
-
Scan #27

Page 16
-
Scan #28

Page 17
-
Scan #29

Page 18
-
Scan #30

Page 19
-
Scan #31

Page 20
-
Scan #32

Page 21
-
Scan #33

Page 22
-
Scan #34

Page 23
-
Scan #35

Page 24
-
Scan #36

Page 25
-
Scan #37

Page 26
-
Scan #38

Page 27
-
Scan #39

Page 28
-
Scan #40

Page 29
-
Scan #41

Page 30
-
Scan #42

Page 31
-
Scan #43

Page 32
-
Scan #44

Page 33
-
Scan #45

Page 34
-
Scan #46

Page 35
-
Scan #47

Page 36
-
Scan #48

Page 37
-
Scan #49

Page 38
-
Scan #50

Page 39
-
Scan #51

Page 40
-
Scan #52

Page 41
-
Scan #53

Page 42
-
Scan #54

Page 43
-
Scan #55

Page 44
-
Scan #56

Page 45
-
Scan #57

Page 46
-
Scan #58

Page 47
-
Scan #59

Page 48
-
Scan #60

Page 49
-
Scan #61

Page 50
-
Scan #62

Page 51
-
Scan #63

Page 52
-
Scan #64

Page 53
-
Scan #65

Page 54
-
Scan #66

Page 55
-
Scan #67

Page 56
-
Scan #68

Page 57
-
Scan #69

Page 58
-
Scan #70

Page 59
-
Scan #71

Page 60
-
Scan #72

Page 61
-
Scan #73

Page 62
-
Scan #74

Page 63
-
Scan #75

Page 64
-
Scan #76

Page 65
-
Scan #77

Page 66
-
Scan #78

Page 67
-
Scan #79

Page 68
-
Scan #80

Page 69
-
Scan #81

Page 70
-
Scan #82

Page 71
-
Scan #83

Page 72
-
Scan #84

Page 73
-
Scan #85

Page 74
-
Scan #86

Page 75
-
Scan #87

Page 76
-
Scan #88

Page 77
-
Scan #89

Page 78
-
Scan #90

Page 79
-
Scan #91

Page 80
-
Scan #92

Page 81
-
Scan #93

Page 82
-
Scan #94

Page 83
-
Scan #95

Page 84
-
Scan #96

Page 85
-
Scan #97

Page 86
-
Scan #98

Page 87
-
Scan #99

Page 88
-
Scan #100

Page 89
-
Scan #101

Page 90
-
Scan #102

Page 91
-
Scan #103

Page 92
-
Scan #104

Page 93
-
Scan #105

Page 94
-
Scan #106

Page 95
-
Scan #107

Page 96
-
Scan #108

Page 97
-
Scan #109

Page 98
-
Scan #110

Page 99
-
Scan #111

Page 100
-
Scan #112

Page 101
-
Scan #113

Page 102
-
Scan #114

Page 103
-
Scan #115

Page 104
-
Scan #116

Page 105
-
Scan #117

Page 106
-
Scan #118

Page 107
-
Scan #119

Page 108
-
Scan #120

Page 109
-
Scan #121

Page 110
-
Scan #122

Page 111
-
Scan #123

Page 112
-
Scan #124

Page 113
-
Scan #125

Page 114
-
Scan #126

Page 115
-
Scan #127
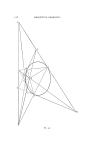
Page 116
-
Scan #128

Page 117
-
Scan #129

Page 118
-
Scan #130

Page 119
-
Scan #131

Page 120
-
Scan #132

Page 121
-
Scan #133

Page 122
-
Scan #134

Page 123
-
Scan #135

Page 124
-
Scan #136

Page 125
-
Scan #137

Page 126
-
Scan #138

Page 127
-
Scan #139

Page 128
-
Scan #140

Page 129
-
Scan #141

Page 130
-
Scan #142

Page 131
-
Scan #143

Page 132
-
Scan #144

Page 133
-
Scan #145

Page 134
-
Scan #146

Page 135
-
Scan #147

Page 136
-
Scan #148

Page 137
-
Scan #149

Page 138
-
Scan #150

Page 139
-
Scan #151

Page 140
-
Scan #152

Page 141
-
Scan #153

Page 142
-
Scan #154

Page 143
-
Scan #155

Page 144
-
Scan #156

Page 145
-
Scan #157

Page 146
-
Scan #158

Page 147
-
Scan #159

Page 148
-
Scan #160

Page 149
-
Scan #161

Page 150
-
Scan #162

Page 151
-
Scan #163

Page 152
-
Scan #164

Page 153
-
Scan #165

Page 154
-
Scan #166

Page 155
-
Scan #167

Page 156
-
Scan #168

Page 157
-
Scan #169

Page 158
-
Scan #170

Page 159
-
Scan #171

Page 160
-
Scan #172

Page 161
-
Scan #173

Page 162
-
Scan #174

Page 163
-
Scan #175

Page 164
-
Scan #176

Page 165
-
Scan #177

Page 166
-
Scan #178

Page 167
-
Scan #179

Page 168
-
Scan #180

Page 169
-
Scan #181

Page 170
-
Scan #182

Page 171
-
Scan #183

Page 172
-
Scan #184

Page 173
-
Scan #185

Page 174
-
Scan #186

Page 175
-
Scan #187

Page 176
-
Scan #188

Page 177
-
Scan #189

Page 178
-
Scan #190

Page 179
-
Scan #191

Page 180
-
Scan #192

Page 181
-
Scan #193

Page 182
-
Scan #194

Page 183
-
Scan #195

Page 184
-
Scan #196

Page 185
-
Scan #197

Page 186
-
Scan #198

Page 187
-
Scan #199

Page 188
-
Scan #200

Page 189
-
Scan #201

Page 190
-
Scan #202

Page 191
-
Scan #203
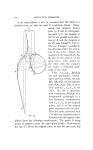
Page 192
-
Scan #204

Page 193
-
Scan #205

Page 194
-
Scan #206

Page 195
-
Scan #207

Page 196
-
Scan #208

Page 197
-
Scan #209

Page 198
-
Scan #210

Page 199
-
Scan #211

Page 200
-
Scan #212

Page 201
-
Scan #213

Page 202
-
Scan #214

Page 203
-
Scan #215

Page 204
-
Scan #216

Page 205
-
Scan #217

Page 206
-
Scan #218

Page 207
-
Scan #219

Page 208
-
Scan #220

Page 209
-
Scan #221

Page 210
-
Scan #222

Page 211
-
Scan #223

Page 212
-
Scan #224

Page 213
-
Scan #225

Page 214
-
Scan #226

Page 215
-
Scan #227

Page 216
-
Scan #228

Page 217
-
Scan #229

Page 218
-
Scan #230

Page 219
-
Scan #231

Page 220
-
Scan #232

Page 221
-
Scan #233

Page 222
-
Scan #234

Page 223
-
Scan #235

Page 224
-
Scan #236

Page 225
-
Scan #237

Page 226
-
Scan #238

Page 227
-
Scan #239

Page 228
-
Scan #240

Page 229
-
Scan #241

Page 230
-
Scan #242

Page 231
-
Scan #243

Page 232
-
Scan #244

Page 233
-
Scan #245

Page 234
-
Scan #246

Page 235
-
Scan #247

Page 236
-
Scan #248

Page 237
-
Scan #249

Page 238
-
Scan #250

Page 239
-
Scan #251
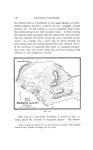
Page 240
-
Scan #252

Page 241
-
Scan #253

Page 242
-
Scan #254

Page 243
-
Scan #255

Page 244
-
Scan #256

Page 245
-
Scan #257

Page 246
-
Scan #258

Page 247
-
Scan #259

Page 248
-
Scan #260

Page 249
-
Scan #261

Page 250
-
Scan #262

Page 251
-
Scan #263

Page 252
-
Scan #264

Page 253
-
Scan #265

Page 254
-
Scan #266

Page 255
-
Scan #267

Page 256
-
Scan #268

Page 257
-
Scan #269

Page 258
-
Scan #270

Page 259
-
Scan #271

Page 260
-
Scan #272

Page 261 - Comprehensive Index
-
Scan #273

Page 262 - Comprehensive Index
-
Scan #274

Page 263 - Comprehensive Index
-
Scan #275

Page 264 - Comprehensive Index
-
Scan #276

Page 265 - Comprehensive Index
-
Scan #277

Page 266 - Comprehensive Index
-
Scan #278

Page 267 - Comprehensive Index
-
Scan #279

Page #279
-
Scan #280

Page #280
-
Scan #281

Page #281
Actions
About this Item
- Title
- An introduction to projective geometry and its applications; an analytic and synthetic treatment, by Arnold Emch ...
- Author
- Emch, Arnold, b. 1871.
- Canvas
- Page 250
- Publication
- New York,: J. Wiley & sons; [etc., etc.]
- 1905.
- Subject terms
- Geometry, Projective
- Geometry, Analytic -- Plane
Technical Details
- Link to this Item
-
https://name.umdl.umich.edu/aas4074.0001.001
- Link to this scan
-
https://quod.lib.umich.edu/u/umhistmath/aas4074.0001.001/277
Rights and Permissions
The University of Michigan Library provides access to these materials for educational and research purposes. These materials are in the public domain in the United States. If you have questions about the collection, please contact Historical Mathematics Digital Collection Help at [email protected]. If you have concerns about the inclusion of an item in this collection, please contact Library Information Technology at [email protected].
DPLA Rights Statement: No Copyright - United States
Related Links
IIIF
- Manifest
-
https://quod.lib.umich.edu/cgi/t/text/api/manifest/umhistmath:aas4074.0001.001
Cite this Item
- Full citation
-
"An introduction to projective geometry and its applications; an analytic and synthetic treatment, by Arnold Emch ..." In the digital collection University of Michigan Historical Math Collection. https://name.umdl.umich.edu/aas4074.0001.001. University of Michigan Library Digital Collections. Accessed May 19, 2025.