Abstract

Importance:

As a mathematical tool, graph analysis provides a way to understand changes in the brains of individuals with Alzheimer’s disease and its associated devastating cognitive decline.

Observations:

The brain may be considered a network consisting of different brain regions that transfer information through connections. Graph analysis is an emerging technique that describes networks in terms of different properties, and the concepts may be applied readily to human brain networks. In healthy subjects, changes in brain network properties correlate with differences in cognition. A number of studies have sought to elucidate the observed disconnectivity in Alzheimer’s disease and how network properties are affected. Using a variety of imaging techniques to construct networks, researchers have used graph analysis to demonstrate changes in the brains of patients with Alzheimer’s disease, including losses in efficiency and integrative ability. A number of these changes correlate with losses of cognitive function.

Conclusion and Relevance:

Graph analysis comprehensively describes brain network changes, and in the future, both researchers and clinicians could employ its techniques to better understand and treat Alzheimer’s disease.

Introduction to Graph Theory in Neurological Networks

Importance and Organization

Despite study of the topic for more than 100 years,[1] much about Alzheimer’s disease (AD) has yet to be elucidated fully. As the number of individuals with AD continues to increase, a better understanding of the disease is warranted. One approach is to attempt to understand changes in the AD brain using graph analysis.[2] Graph analysis is a mathematical technique that first expresses a system as a network, which consists of regions and connections between those regions, and then compares the properties of the networks. When applied to the brain, which can be described as a network based on anatomical regions, graph analysis allows researchers to compare immensely complex systems using relatively simple measures.[3] Further details of this technique will be introduced later in this review. A number of scientific articles have applied graph analysis to study AD, and synthesis of these findings could improve understanding of the disease and provide future advantages in treatment and prognosis.

This review attempts to summarize the articles that have used graph analysis to compare different groups in the context of AD. Following an introduction of the brain as a network, graph analysis, and AD, this review will delve into the comparative studies. The studies are organized by the imaging modality used to construct the brain networks. Finally, this review will discuss the rationale for differences observed in the results of the studies as well as future directions for research.

The Brain as a Network

The brain may be considered an intricately complex and incredibly efficient network composed of up to 100 or more anatomical brain regions.[3] These regions have specialized functions and are in constant communication with one another via physical connections, such as axons, and functional connections, such as synchronicity in neural activity.[4] Information is processed locally among nearby regions and globally between distant structures, and it is this combination of parallel processing and powerful integrative ability that makes the human brain unique.[3] Studying the network properties of the brain may elucidate key information regarding health and disease.

Brain regions may be connected physically through either direct structural connections or similarities in structural composition. Diffusion tensor imaging (DTI) has emerged as the predominant method to study white matter tracts in the brain. Researchers can use DTI and tractography to reconstruct axonal tracts and thus determine physical connectivity between brain regions.[5] Networks of these tracts can be characterized and studied. Alternatively, researchers can construct networks based on the structure of gray matter, which can be analyzed with high resolution using structural magnetic resonance imaging (sMRI). Based on the assumption that related regions share similar morphology, investigators can generate brain networks based on physical similarities such as cortical thickness and gray matter volume.[6]–[8] In this technique, connected brain regions may or may not be linked by a white matter tract.

Networks also may be constructed via functional connectivity, which is based on communication between anatomically distinct regions. With this approach, brain regions that are active at the same time are considered functionally connected.[9] Electroencephalography (EEG), magnetoencephalography (MEG), and functional magnetic resonance imaging (fMRI) all have been used to construct networks using synchronicity in brain region activity.[10]–[12] In EEG and MEG, correlations are determined using the activity at different frequency bands, whereas in fMRI, correlations are based on blood–oxygen–level dependent (BOLD) contrasts. In resting–state measurements, brain regions are still active, although the patient is “at rest” and not performing any tasks. Using fMRI, patterns in the BOLD response have identified consistent resting–state networks (RSNs) composed of regions that are active in unison.[13] Of the RSNs, the default–mode network (DMN) has gained a large amount of research attention. The DMN has been related to a number of cognitive processes, including monitoring the world,[14] the integration of cognitive and emotional processing,[15] and mind–wandering,[16] and the integrity of the DMN affects cognition.[17] Finally, positron emission tomography (PET) can be used to determine functional connectivity based on similarities in metabolism.[18] Neuronal activity is related to glucose metabolism, and thus PET measurements of glucose metabolism reflect brain activity.

Graph Theory and Analysis

To study the brain as a network, it is helpful to employ an analytical technique that can assess the properties of such a network system, and the technique should be broad enough to encompass many different ways in which networks can be defined. With these requirements, graph theory has emerged as a descriptive method, and graph analysis provides accompanying ways to interpret network differences. Graph theory is a mathematical representation that decomposes networks, which alternatively are named graphs, into nodes and edges. Nodes represent distinct points such as positions in space, and edges are the constructs that connect them. Edges are most simply nondirectional and unweighted, but they may be directional and/or weighted. Directional means that the edge implies some relationship within the connection, and weighted means that the edge provides information about the strength of the connection. Previous researchers have defined a number of further parameters that describe networks. See Table 1 for a list of parameters and their definitions.[19]–[22] Figure 1 depicts a number of these concepts.

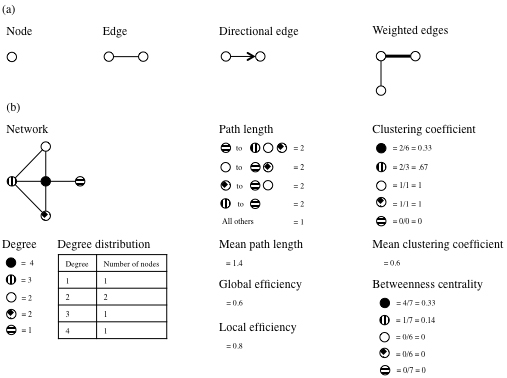
FIGURE 1. (a) Illustrates graph theory constructs and (b) provides example measures for parameters discussed in this review.
FIGURE 1. (a) Illustrates graph theory constructs and (b) provides example measures for parameters discussed in this review.
TABLE 1. Common Parameters Used in Graph Analysis to Describe Networks
ParameterDefinition
DegreeThe number of connections from the node of interest to other nodes of the network
Degree distributionThe degrees of all the nodes within the network
Path lengthThe minimum number of edges that must be traversed to reach from one node of interest to another
Mean path lengthThe average path length to travel between all combinations of nodes
Global efficiencyThe average of the inverse of the path length for all nodes
Local efficiencyThe average global efficiency of subgraphs for each node containing the neighbors of that node
Clustering coefficientThe number of connections between the nearest neighbors of a node proportional to the maximum number of connections
Mean clustering coefficientThe average clustering coefficient of all nodes
Betweenness centralityThe proportion of shortest paths between any 2 nodes that pass through this node

Nodes with high clustering coefficients or high betweenness centrality are termed hubs. Hubs are crucial nodes within a network because a relatively high amount of information is transferred through them, and they are necessary for efficient communication.[19] Interactions between nodes also can be assessed by modularity, which is a measure of how the network is organized into modules (communities of nodes) with high levels of local clustering.[23] Depending on the study, different definitions of modularity exist.[23],[24] The strength of modularity is based on the relation between intermodule and intramodule connections.

Watts and Strogatz recognized that some networks exhibit common patterns, and their work revolutionized the use of graph theory.[20] Their pioneering paper outlined 3 types of networks within a spectrum. At one extreme, regular networks are characterized by extremely ordered lattices and high clustering but long path lengths. At the other end of the spectrum, random graphs are highly disordered and have low clustering but short path lengths. In the middle lie small–world networks, characterized by a relatively high degree of order but also a number of long–range connections, resulting in networks with high clustering and low path lengths. See Figure 2 for a depiction of these 3 network architectures.

FIGURE 2. Three example networks in the spectrum of architectures.
FIGURE 2. Three example networks in the spectrum of architectures.

Small–world networks allow for efficient communication within local clusters as well as rapid interregional communication. They thus exhibit high values for global efficiency and local efficiency. The small–world measure is defined as the clustering coefficient divided by the path length, and a network is considered “small–world” if this measure is greater than 1. Watts and Strogatz recognized that a number of real–world biological, technological, and social networks are in fact small–world. It was not long before investigators sought to apply such ideas to the human brain network.

A small–world network structure enables efficient parallel processing and fast interregional communication, and fluctuating brain network interactions could provide the ability to perform tasks by balancing brain activity between local differentiation and global integration. Following the work of Watts and Strogatz, a number of imaging studies have demonstrated that the human brain exhibits properties of a small–world network. Functional connectivity studies have used EEG,[25] MEG,[26] fMRI,[27] and PET,[28] while structural connectivity studies have used DTI[29] and sMRI.[6]–[8] It has been demonstrated that neuronal dynamics obey a highly modular architecture,[30] and performing certain tasks is accompanied by characteristic changes in interactions between neural networks. These findings support the concept that distinct brain regions and networks play specific roles in certain brain functions.[31] The uniquely powerful small–world architecture thus may be instrumental in brain performance.

Cognition in Healthy Subjects and Graph Analysis

Networks from brains of all ages exhibit modular organization with greater connectivity within the modules than between them, which is characteristic of small–world architecture.[32] This small–world architecture is conducive to performing cognitive tasks, and it has been observed that the properties of brain networks correlate with differences in cognition. For example, significant correlations have been observed between intelligence quotient scores and network properties.[33] Smaller path length and higher global efficiency measures, which characterize efficient information transfer in the brain, corresponded to higher intelligence scores.

If the network properties of the brain are fine–tuned, architectural changes reasonably could affect cognitive ability. Even in the absence of overt disease, network properties of the brain evolve with time, and it may be that the decline of cognition with age is in part due to alterations in network properties.[34],[35] Cortical connectivity decreases with age, and the efficiency of the brain network decreases.[36],[37] This decrease in efficiency appears to be reduced disproportionately to connection cost.[38] The brains of older adults have longer path lengths compared to those of younger adults, principally due to the loss of long–range connections.[35] Brains of older individuals also show higher local clustering[34] with decreased intermodule connections.[37] These alterations indicate a shift toward more local organization in older age. The ability to integrate information on a global level may be compromised due to this switch toward stronger local communication.

Age–related connectivity changes and reductions in functional segregation are most prominent in regions that are important for cognition. Older brains show reduced intermodule connectivity in the executive function network, DMN, and frontal modular regions,[39],[40] while decreases in efficiency are highest in frontal regions.[38] Furthermore, regional betweenness centrality, which indicates to some degree the importance of networks hubs, is reduced in frontal regions of older subjects.[35] Other regions exhibit changes in betweenness centrality, including increases in some structures of the DMN[35] and reductions in the hippocampus and insula.[34] Disturbances in network architecture lead to less–optimal network properties, and it is intriguing that these changes occur most prominently in regions important for cognition. Given the impact of normal aging on brain networks and correlations with cognition, it seems reasonable to investigate changes of network properties in diseased states.

Alzheimer’s Disease and Disconnection

AD is characterized by cognitive and functional decline and is the most common neurodegenerative disorder, accounting for 50% to 70% of all dementia cases.[41] AD is a progressive disease in which symptoms gradually worsen over time across cognitive domains such as memory, language, and attention.[42]–[45] Mild cognitive impairment (MCI) is considered a prodromal stage of AD. In MCI, symptoms are not severe enough to warrant an AD diagnosis, although approximately 10% to 15% of MCI patients convert to AD each year.[46] The pathological consequences of AD include cortical and subcortical atrophy, the loss of white matter integrity, and the accumulation of protein abnormalities such as neurofibrillary tangles and amyloid beta plaques.[47] Meanwhile, cognitive changes often are tracked using specific cognitive tests or the Mini–Mental State examination (MMSE), which is a simple, brief test used to assess overall cognition in dementia.[48]

It has been proposed that AD is as a disconnection syndrome in which hub damage and disconnection result in brain network impairment and ultimately cognitive dysfunction.[49] Thus there is an emerging interest in studying connectivity and the impact of AD on networks. In particular, hubs are under scrutiny, as they play a crucial role within the small–world architecture of a network. These points are vital for efficient communication within and between modules. Hub integrity thus is important for the integrity of the whole network: Disruption of a few key nodes can lead to massive changes in the comprehensiveness and efficiency of a network. If a brain lacks proper connections, it may lose the abilities of efficient local processing and global integration. A disrupted brain network may not operate optimally, and cognitive dysfunction could ensue.

Researchers have identified and characterized a number of hubs in the human brain network,[29],[50] and the brain regions most strongly affected in AD include the cortical and subcortical hubs.[51],[52] In AD, damage is nonrandom and the disruption of networks follows a targeted attack model in which hubs are impaired selectively.[53] Pathologically, amyloid beta deposits most heavily at cortical hubs.[54],[55] Furthermore, hubs exhibit hypometabolism in AD.[52] Even in the absence of AD, hubs show decreased metabolism in amyloid–positive subjects.[56] Decreased activation at the hubs may account for decreases in functional connectivity. EEG studies have demonstrated a loss of functional interactions and band synchronization in AD.[57],[58] AD subjects show a loss of long–distance interactions, particularly frontal and parietal connections,[59] as well as anterior and posterior connections.[60] The modular architecture of the brain is affected by these changes, and some of the major modules have been found to fracture into pieces.[61] Some RSNs exhibit reduced efficiency as well as changes in their importance and usage.[62] Deactivation at certain hubs is less pronounced in MCI, which suggests evolution of brain networks with worsening AD pathology.[63] Thus changes in the network may reflect adaptations throughout the disease course. While it is evident that AD affects connectivity, the exact nature of these changes remains unclear.

The cognitive deficits that occur in AD may result from a breakdown in the brain’s unique abilities to access and process information. Pathologic changes disrupt hubs and change connectivity, and these alterations may hamper information processing and integration. This model bears support from multiple studies and techniques. In AD, decreased fMRI functional connectivity of the DMN is correlated with decreased cognition,[64] while changes in MEG alpha and beta band synchronization correlate with MMSE scores.[59],[65] Many studies have been conducted evaluating connectivity in AD, but a major difficulty in reviewing this approach is the enormous variances in measurements, techniques, brain locations, and other aspects of the studies. Graph analysis provides a useful and more concise way to summarize connectivity changes in AD, particularly when examining the brain network at a global level. Moreover, graph analytical measures can be readily correlated with cognitive measures. For these reasons, this work will focus on graph analysis.

Methods

A literature search was conducted using PubMed with combinations of the following keywords: Alzheimer’s disease, graph analysis, and graph theory. Only complete articles written in English were included. From the returned articles, only articles that used graph analysis to compare multiple groups (eg, Alzheimer’s disease and control) were analyzed. See Table 2 for a summary of imaging modalities and articles cited in this review.

TABLE 2. Imaging Modalities of Studies Conducted on Graph Analysis in AD
ModalityStudies
EEGStam et al, 2007[25]
de Haan et al, 2009[53]
Vecchio et al, 2015[67]
MEGStam et al, 2009[26]
De Haan et al, 2012[24]
fMRISupekar et al, 2008[71]
Sanz-Arigita et al, 2010[74]
Zhao et al, 2012[75]
Kim, et al, 2015[76]
Toussaint et al, 2014[17]
Ciftçi 2011[79]
PETSeo et al, 2013[81]
Sanabria-Diaz et al, 2013[28]
DTILo et al, 2010[82]
sMRIHe, Chen, and Evans 2008[83]
Li et al, 2012[84]
Phillips et al, 2015[85]
Yao et al, 2010[86]
Tijms et al, 2013[87]
Carmeli et al, 2014[88]

Alzheimer’s Disease and Graph Analysis

Electroencephalography

Stam et al used EEG to determine connectivity and to analyze network measures in the beta band.[25] Nodes were created from 21 EEG channels, and the edges were determined by measuring and thresholding the synchronization likelihood[66] of the nodes. Stam et al observed that the mean path length was significantly longer in AD subjects compared to controls, although there was no difference in the clustering coefficient. To verify that the change in path length reflected an actual change in the organization of the network and not merely a decrease in functional connectivity, the path length was computed as a function of the mean degree of the network. The AD subjects still had a significantly longer path length than the control subjects. Thus the increase in path length in AD indicated a loss of complexity in the network and suboptimal organization. Moreover, the path length correlated significantly with the MMSE scores of the 2 groups. Stam et al reasoned that compromised network organization in AD, manifested by the increase in path length, might in part explain cognitive dysfunction.

Using EEG methods similar to Stam et al,[25] de Haan et al calculated a number of graph analytical measures across a range of frequencies and observed results dissimilar to those of Stam et al.[53] In the work of de Haan et al, the synchronization likelihood threshold was chosen so that the mean degrees of both groups were equal. Furthermore, to better handle disconnected nodes, a different algorithm was used to determine path length.[23] Compared to the control subjects, the AD subjects had a decreased path length in the lower alpha and gamma bands and a decreased clustering coefficient in the lower alpha and beta bands. In the lower alpha band, the path length was correlated with the MMSE score. Decreases in both path length and clustering shift a network structure away from small–world architecture and toward a more random architecture. De Haan et al reasoned that in optimal cognition, the overall structure of the brain must balance local processing and global integration. Thus the observed randomization of the network in AD may be disadvantageous for cognition.

In an effort to link structural alterations with changes in functional connectivity, Vecchio et al performed EEG and DTI on healthy control, MCI, mild AD, and moderate AD subjects.[67] For the EEG brain networks, 19 electrodes were used to generate 84 nodes corresponding to Brodmann areas[68] in standardized space. Edges were defined based on lagged linear coherence in the delta and alpha 1 frequency bands. DTI data were used to calculate the fractional anisotropy (FA), a measure of white matter tract integrity, of 19 anatomically selected white matter segments. There was an observed decrease in corpus callosal FA in the AD group, indicating a loss of structural integrity in those tracts. Moreover, grouping all subjects together, the splenius callosal FA and the path length were negatively correlated in the delta band and positively correlated in the alpha 1 band. It has been demonstrated previously that for path length, a simultaneous increase in low–frequency bands and a decrease in the alpha band are associated with an increase in brain disconnection.[69] Thus Vecchio et al reasoned that the loss of white matter structural integrity in AD might be at least partially at fault for network disruption.

Magnetoencephalography

Stam et al used MEG and graph analysis to study brain networks in AD and healthy control subjects.[26] One hundred forty–nine MEG channels were used as nodes, and weighted edges were determined by the phase lag index, which has been demonstrated to perform at least as well as the synchronization likelihood.[70] To negate the effects of network size, the clustering coefficient and path length were normalized by dividing the obtained values by those of random networks with reshuffled edge weights. In the lower alpha band, the normalized clustering coefficient and normalized path length were decreased in AD subjects. Supporting earlier findings using EEG,[53] these changes suggest a randomization of networks in AD. Moreover, AD subjects showed a decrease in synchronization in the lower alpha and beta bands. The loss in synchronization affected regions heterogeneously, as there was a preferential decrease of connections between hubs. These findings suggest a targeted disruption of network structure, which may be responsible for the randomization of networks. For all subjects, mean synchronization correlated with MMSE scores in the beta band, and the normalized clustering coefficient correlated with MMSE scores in the lower alpha band. Together with the findings of shorter path length and decreased clustering coefficient in AD, these correlations suggest that the randomization of networks in AD impairs cognition.

De Haan et al assessed modularity in AD using MEG.[24] One hundred forty–nine channels were used as nodes, and edges were defined by nonthresholded synchronization likelihood. Intramodular strength was quantified by within–module degree, which describes the relative importance of the node within the module. Intermodular strength was quantified by the participation coefficient, which expresses how strongly a node is connected to other modules. Compared to control subjects, AD subjects had higher modularity in the delta and theta bands and lower modularity in the beta and gamma bands. Moreover, intramodular strength was decreased in the beta band, and intermodular strength was decreased in the delta and theta bands. The increase in modularity of the delta and theta bands can be explained by the severe decrease in intermodular strength in these bands, which corresponds to a massive loss of intermodular connections. This decreased modularity and connectivity in AD indicates significant disruption from the healthy brain network, which relies on division and integration of data processing. In the AD group, several graph analytical measures correlated with neuropsychological test scores: delta band modularity and fluency, intermodular strength and word recall, intermodular strength and fluency, lower alpha band modularity and visual recognition, intermodular strength and visual recognition, and intermodular strength and fluency. The observed differences were related to worse cognitive performance, indicating that changes in network architecture with AD result in suboptimal cognitive conditions.

Functional Magnetic Resonance Imaging

Supekar et al used fMRI data to study functional connectivity and network changes in AD.[71] Based on the automated anatomical labeling (AAL) atlas,[72] 90 brain regions were defined as nodes. Edges were determined by thresholding wavelet correlation matrices.[73] The individual correlation matrices were thresholded to ensure equal mean degrees of the networks. In the frequency interval between 0.01 and 0.05 Hz, the clustering coefficient and small–world measure were significantly lower in the AD group compared to the control group. While the mean path lengths and global efficiencies were also lower in AD, the differences were not significant. Based on regional measures, the clustering coefficient was significantly lower in the hippocampus, a structure important for cognition. The decreased clustering coefficient, decreased small–world measure, and other data trends indicate a randomization of the network and a loss in local efficiency in AD.

Sanz–Arigita et al used fMRI and graph analysis to investigate AD and the impact of network changes on cognition.[74] Nodes were defined by 116 anatomical regions, and edges were defined using synchronization likelihood. In groups of AD and healthy control subjects, the mean path length and clustering coefficient were calculated as a function of the mean degree. The mean path length of the AD group was significantly lower, and no difference was observed in the clustering coefficient. Alterations in regional connectivity in the AD subjects may explain the reduced path length, as there was a loss of long–distance connections and a relative increase in intramodular connections. This increased randomization of the network would reduce path length. Although a trend toward lower a MMSE score was observed with lower mean path length, the correlation was not significant.

Using a similar setup to the previously mentioned study by Supekar et al,[71] Zhao et al investigated graph analytical changes in subjects with moderate AD.[75] Edges were defined using the Pearson correlation between 0.01 and 0.08 Hz. The clustering coefficient, path length, and local efficiency were increased in AD subjects, and the global efficiency was decreased. The longer path length and lower global efficiency suggest that information integration between regions is impaired in AD. These results seemingly contradict earlier findings, although Zhao et al cited a number of methodological reasons for the discrepancies between their results and those of Supekar et al[71] and Sanz–Arigita et al.[74] A later section of this review features a more detailed discussion of the differences in results.

To elucidate network properties of various stages of AD, Kim et al analyzed fMRI networks among 5 groups, which were stratified using the clinical dementia rating (CDR): healthy control, MCI, AD (CDR = 0.5), AD (CDR = 1.0), and AD (CDR = 2.0).[76] The CDR is a rating scale that is performed by a physician and broadly describes the level of cognitive impairment; a higher score indicates more impairment.[77] The AAL atlas was used to define 90 nodes, and edges were generated by mutual information. Mutual information is a measure of the joint probability distribution of 2 nodes, which factors in the marginal probability distributions of each.[76] The results demonstrated an ongoing reorganization process among the 5 groups, although surprisingly the reorganization occurred in a nonmonotonic manner. Local efficiency, global efficiency, and betweenness centrality all demonstrated statistically significant differences among the groups. Among the 5 groups, these 3 measures peaked in the MCI and AD (CDR = 1.0) groups. No graph analytical measure correlated with clinical deterioration as measured by CDR. Kim et al reasoned that the observed differences and nonmonotonic pattern might be explained in part by compensatory mechanisms. At least for the MCI subjects, the increase in graph analytical measures may be a result of hyperactivation of the hippocampus and other memory–related areas, which would result in reorganization of the brain network.[78] It is possible that the differences observed in the study reflect remodeling that takes place in the progressively altered AD brain.

Toussaint et al analyzed the DMN more specifically in their fMRI comparison of healthy elderly controls and subjects with AD.[17] Ten anatomical regions within the DMN were defined as nodes, and a thresholded correlation matrix was used to generate edges. The clustering coefficient and the degree of nodes across the DMN were reduced in the AD group, although statistical significance was reached only at the level of the precuneus–posterior cingulate area. These results indicate decreased network integration in AD that may be particularly prominent in the posterior cingulate cortex.

In an alternate approach to traditional graph analytical approaches, Ciftçi analyzed the minimum spanning tree (MST) in the DMN using fMRI.[79] The MST of a graph connects all nodes at a minimal cost of connections. Ciftçi reasoned that brain networks are cost–effective and that pathological alterations may result in networks that show less cost–effectiveness. The data were collected during a simple sensory–motor task. Nodes were derived from 32 regions in the AAL atlas that are part of the DMN. Edges were determined by the frequency bootstrap method, in which surrogate time series are calculated from the inverse spectrum of the power spectra, and correlation is based on bootstrap pairs.[80] The DMN of the AD group showed more fragmented functioning than that of the control group, as the posterior cingulate/precuneus complex and the hippocampus/parahippocampus complex were isolated from rest of the network. The results suggest that structures related to cognition within the DMN become more segregated in AD.

Proton Emission Tomography

Seo et al assessed MCI and AD using graph theory and glucose metabolism measured by PET.[81] For some of the analysis, the AD group was divided into 2 subgroups based on dementia severity: “very mild AD” (CDR = 0.5) and “mild AD” (CDR = 1.0). Metabolism of [18F] fluorodeoxyglucose (FDG) was measured, and values were normalized based on the mean global metabolic rate. Nodes were defined by 90 regions from the AAL atlas, and a correlation matrix was used to determine edges. Connectivity values were thresholded based on sparsity, which is defined as the total degree divided by the total possible degree. Mean path length and clustering coefficient were normalized by values of random networks with the same distribution density. Both the AD group and the MCI group had significantly lower clustering coefficients than the control group, and at certain sparsity thresholds the value of the MCI group was lower than that of the AD group. There were no differences in path length between the control group and the other 2 groups, although at certain sparsity thresholds the path length was longer in the AD group than in the MCI group. In the subgroup analysis, the mild AD subgroup had a larger clustering coefficient and a longer path length than the very mild AD subgroup. In addition, connectivity was reduced in prefrontal regions in the AD group and the MCI group. Seo et al reasoned that the unexpected finding that clustering was more disrupted in MCI than AD can be explained by the patterns of regional hypometabolism. The MCI group had scattered and focal impairment, whereas the AD group had diffuse impairment. Since local clustering is based on correlations between adjacent regions, this value was affected more profoundly in MCI. Hypometabolism appeared to extend to further brain regions as AD progressed, resulting in the restoration of the clustering coefficient. This conclusion is supported by the subgroup analysis. The results demonstrate a progressive disruption of small–world architecture that evolves with the course of AD. In particular, longer path lengths and lower clustering characterize the networks of diseased brains.

Sanabria–Diaz et al similarly analyzed glucose metabolism networks with PET.[28] Metabolic rates were normalized using the brainstem as a reference cluster. The connectivity matrix was augmented with bootstrapping, and edges were determined using the Pearson correlation coefficient and thresholded by sparsity values. The AD group had significantly longer path length, clustering coefficient, and local efficiency values than the MCI group and control group, and the MCI group had middling values for all those measures. The AD group had lower global efficiency than the MCI group and control group, and the small–world measure of the control group was significantly higher than the values of the other 2 groups. The results indicate disruption in small–world architecture toward a more regular network. Further, there appear to be progressive changes in the disease with MCI as a prodromal stage of AD. In addition, hub regions, which were identified based on betweenness centrality in the control group, showed relatively greater hypometabolism and reduced connectivity in the AD and MCI groups. This suggests that hubs are targeted in AD pathology, and this process may cause the deviation from small–world architecture. The regularization of brain networks in AD indicates imbalance between network segregation and integration processes.

Diffusion Tensor Imaging

In contrast to the aforementioned works that used functional connectivity, Lo et al used DTI to analyze structural connectivity in the brain and correlate graph analytical measures to cognition.[82] Nodes were defined based on 78 brain regions in the AAL atlas. Edges were generated based on tractography of the DTI data: If there were at least 3 white matter fibers connecting the affiliated regions, then an edge weighted by the number of fibers was established. The weighted mean path length and weighted clustering coefficient were normalized by dividing by the mean values of random networks of the same size and degree. In the AD group compared to the control group, the mean path length was significantly longer and the global efficiency was significantly lower. The AD group also had reduced nodal efficiency, particularly in the frontal regions. Moreover, in the AD group, the mean path length, clustering coefficient, and global efficiency were correlated with neuropsychological test scores assessing verbal memory. These findings indicate that changes in the physical brain network structure have consequences for cognition, and disruption of small–world architecture with AD may result in suboptimal cognitive function.

Structural Magnetic Resonance Imaging

He, Chen, and Evans used sMRI and graph analysis to study AD.[83] To define nodes, cortical thickness was measured and mapped, and the maps were parcellated for each group into an average of 54 regions. Correlation matrices of the groups were computed and then were binarized to define the edges. The thresholds were determined so that group networks would have the same sparsity. Both the mean path length and the clustering coefficient were higher in the AD group compared to the control group. Also in the AD group, betweenness centrality was decreased in the lateral temporal and parietal cortices and increased in the unimodal association cortex and paralimbic regions. The increased path length and clustering in AD suggests a more regular network with relatively stronger local specialization.

Li et al used cortical thickness and graph analysis to study 4 groups: healthy control, stable MCI, progressive MCI, and AD subjects.[84] Stable versus progressive MCI was determined based on whether the subjects converted to AD at least 12 months after the study data were collected but prior to the data analysis, a period of up to 6 years. Nodes were derived from 90 regions on the AAL atlas, and edges were based on statistical correlation of the cortical thickness. The clustering coefficient was reduced in both MCI groups and the AD group compared to the control group, although the difference was significant only in the progressive MCI group. These findings suggest that local information processing may be disrupted in AD and its prodromal stages.

Recognizing the discrepancy in published studies of how graph analytical values change with AD, Phillips et al sought to clarify the effects of network definitions on cortical thickness networks in 4 groups: healthy control, stable MCI, progressive MCI, and AD subjects.[85] The cortex of each subject was divided into 68 regions of interest to generate nodes. Edges were defined by statistical associations of cortical thickness.[83] By computing the Pearson correlations differently and optionally controlling for cortical thickness, 8 correlation matrices were constructed for each group. For the graphs that did not control for mean cortical thickness, path length was shortest for the control group, and some of the graphs demonstrated an increase in path length the groups from control to stable MCI to progressive MCI to AD groups. In those same graphs, the clustering coefficient showed the opposite trend: It was highest in the control group and lowest in the AD group. These trends, however, were reversed upon looking at the other graphs. When the Pearson correlations were controlled by cortical thickness, the control group had the longest path length and the AD group the shortest. In the graphs based on absolute partial correlations, the AD group had significantly higher clustering coefficient values compared to the control group. All of these results demonstrated that AD pathology affects routing between brain regions; however, the magnitude and even direction of group findings are affected by the choice of correlation matrix. Different matrices produced graphs with different properties. Phillips et al reasoned that the sparsity threshold and the average connection weight, which are used to determine the edges included in a graph, have significant impacts on the size and connectivity density, which in turn affect graph analytical measures. Furthermore, controlling for cortical thickness or using partial correlations may alter the amount of regional interdependency on pairs of nodes, which also alters graph properties. The findings indicate that changes in network properties in AD are not necessarily straightforward and that thought must be applied when constructing graphs and analyzing disruptions in network function.

Rather than cortical thickness, Yao et al used gray matter volume to measure structural connectivity in AD and MCI.[86] Ninety nodes were based on regions of the AAL atlas, and edges were defined using Pearson correlation coefficients. To control for changes in overall network connectivity, thresholds were based on sparsity. The path length and clustering coefficient were highest for the AD group and smallest for the control group, with the MCI group measurements in between for both; however, only the difference in path length between the AD group and the control group was statistically significant. In addition, betweenness centrality changes were detected in both the MCI group and the AD group, including in some hubs of the DMN. The trends of graph analytical values indicate that the loss of small–world characteristics in AD follows a progressive decline, with MCI as a transitional stage before AD. Furthermore, regions that are important for cognition seem to be affected more significantly by AD pathology.

Tijms et al employed a data–driven approach[7] to generate cortical networks for graph analysis in AD.[87] An average of 8683 nodes was defined individually for each subject based on small regions within the gray matter segmentation. Edges were based on a correlation coefficient that accounted for the geometrical shape and gray matter volume within the regions of interest. The threshold was determined for each graph so as to allow a similar chance of including 5% spurious correlations. The mean path length and clustering coefficient were normalized by dividing by those values from random networks of identical size and degree distribution. The mean path length, clustering coefficient, and small–world measure were decreased significantly in the AD group compared to the control group, reflecting an increased randomization in the network. Moreover, the mean path length was correlated strongly to MMSE scores. In a forward linear regression model, the path length in the left parahippocampal gyrus explained 32% of the variance in cognition. This correlation suggests that the increased randomization of networks in AD leads to suboptimal cognitive conditions and impaired function.

While most of the literature focuses on gray matter networks, Carmeli et al used superficial white matter to construct networks.[88] Seventy–eight nodes were defined by anatomical locations of white matter, and edges were determined based on statistical associations of the magnetization transfer ratio. The magnetization transfer ratio indicates the amount of signal lost due to magnetization transfer, an effect that depends mainly on the myelin concentration. Carmeli et al proposed that graph analysis of magnetization transfer ratio networks could illustrate the effects of demyelination in AD. Compared to the control group, the AD group showed decreased local efficiency, particularly in areas associated with demyelination in AD.[89] Measures of global efficiency and modularity were not statistically different between the 2 groups. These findings indicate that white matter networks are disrupted in AD in similar ways to alterations in gray matter networks.

Differences in Results

From the previous sections, it is obvious that different graph analytical studies present different and even seemingly contradictory results. Several rationalizations have been proposed to remedy the discrepancies. First, many of the differences may arise due to differences in modalities. Networks based on structural or functional connectivity assess different measures, and changes observed using one method might not mirror changes in another. Indeed, functional connections may be independent of direct anatomical connectivity.13 Furthermore, the association between functional connectivity and structural connectivity may be indirect. For example, deactivation of a brain region may result in an observed decrease in functional connectivity to another region. Alternatively, a functional network may show increased connectivity in spite of decreased white matter tract integrity due to compensatory action.[75] Compensatory increases in activation, which may cause increased connectivity, may help maintain functional integrity at distant sites despite the fact that those sites exhibit decreased white matter tract integrity locally. Despite apparent differences in structural versus functional connectivity, it has been suggested that structural changes predominantly underlie functional changes. For instance, using DTI and fMRI, Pineda–Pardo et al showed that many of the observed changes in functional connectivity in MCI correlate to losses of white matter tract integrity.[90]

Even within the realm of functional connectivity, comparing different imaging methods also may be problematic. For instance, EEG and MEG observe only cortical changes in activation, while fMRI can assess subcortical structures. The mapped graphs differ between modalities since the ability to measure interconnectivity is dramatically different. Moreover, the resolution of a graph influences its properties. Network composed of 10 regions may differ greatly from networks composed of hundreds or even thousands of regions. It has been observed that networks with higher resolutions exhibit properties of small–world networks more prominently,[91] and other graph analytical properties may be influenced by network size as well. The network resolution may depend on the modality (eg, EEG is intrinsically less sensitive than MEG) or the individual choices and justifications of the researchers.

Even within the same imaging technique, there may be methodological differences that affect the degree of connectivity between regions and thus graph analytical measures. For example, due to the high amount of atrophy in AD, spatial smoothing can impact results dramatically.[75] Furthermore, how edges are defined and how values are normalized may influence results. Tijms et al demonstrated that the clustering coefficient of one group can be observed as higher or lower than that of another group simply by affecting the threshold of connectivity that defines an edge.[2] The choice of statistical correlation also influences edge definition and thus network properties. The Pearson correlation coefficient, which is used most commonly to determine functional connectivity among fMRI networks, reflects the linear relationship among regions but not the nonlinear relationship. Mutual information, by contrast, accounts for nonlinear interactions.[76] Different choices of statistical correlation may cause different network constructions, which has a profound impact on results. This effect is especially pronounced because AD subjects show more disconnected nodes, and edge definition heavily influences the involvement within a network. The aforementioned factors demonstrate that although the disease process may be the same across different studies, observations may be affected profoundly based on how imaging data are processed.

The composition of the groups may influence observed results as well, as subjects at different stages in the disease course may possess different underlying mechanisms.[92] The network properties of a patient who has advanced AD may have evolved far more than a patient who just developed dementia symptoms. Tijms et al evaluated the single–subject gray matter graph properties and cognitive test performances of 215 AD subjects.[93] Worse performance was correlated with lower clustering coefficient, path length, and betweenness centrality values. This study illustrates that in a given group of AD subjects, graph analytical measures may be quite inhomogeneous. Studies with both AD subjects and MCI subjects provide an approximate evaluation of the evolution of network properties as the disease progresses, and noticeable differences have been observed.[28],[81],[86] Even among MCI patients, differing degrees of impairment may correlate to graph analytical measures. For example, white matter tract organization is disrupted significantly in subjects with multidomain MCI but not in subjects with single–domain MCI.[94] Also, as discussed earlier, differences in graph analytical measures have been observed between groups of progressive and stable MCI subjects.[85] Since subjects at different disease stages may differ substantially, group composition and disease definition are thus important in study design and results interpretation.

Differences at the cellular level also may manifest in different network properties. For instance, the level of amyloid beta deposition in preclinical AD subjects corresponds to changes in graph analytical measures.[95] Cognitively normal subjects with AD pathology showed reduced clustering coefficient and modularity values compared to cognitively normal subjects without AD pathology. The load of amyloid deposition apparently affects networks, and since it is nonrandom, it may influence findings of different subject cohorts.

Future Directions

Evolving technology, imaging methodology, and data processing have broadened the abilities of researchers to assess brain networks and employ graph analysis. One potential application is improving representations of networks. It has been proposed that increasing resolution and defining nodes at smaller brain regions potentially could be more representative of the real system and lead to more accurate assessments.[91] This approach requires increased computation, and in the past, this problem proved difficult to overcome. Li et al proposed a new technique that circumnavigates the problem of heavy computation to construct a voxelwise network with DTI data.[96] The technique employs mathematical theorems to derive values from a network with over a million parameters. The findings using this technique are consistent with previous connectivity studies.[97] Similar computation techniques or advancements in imaging technology could improve the accuracy of calculated networks and yield more results that reflect the real effects of AD.

In the clinic, graph theoretical measures could be used as biomarkers to improve diagnostic accuracy and predictability of cognitive decline. If current research techniques are improved, graph analysis could be employed to aid physicians in prognosis and prepare patients for the future. The normalized clustering coefficient, as determined using fMRI, has been used to diagnose subjects with AD with a sensitivity of 72% and a specificity of 78%.[71] More advanced measures, however, might yield even more promising results. Using EEG and a 2–stage classifier, a sensitivity of 100% and specificity of 91.08% for diagnosis of AD was achieved.[98] Alternatively, Khazaee et al developed a model with 9 graph analytical measures that was predictive for AD diagnosis.[99] In this model, a search–based method was used to generate sparse brain networks and identify nodes with the greatest differences between 20 AD subjects and 20 control subjects, and machine–learning methods were used to construct a model based on the discriminative features. The model was capable of classifying the subjects used to create the model with 100% accuracy. In an expanded study, a model created by Khazaee et al was able to classify 188 subjects into control, MCI, or AD groups with 88.4% accuracy.[100] These results suggest that discriminative network measures potentially could augment current methods in the diagnosis and prognosis of AD, as well as the prediction of progression from MCI to AD.

Additionally, graph analysis potentially could be used to improve treatment plans and treatment assessment. Network measures could be used to identify which patient groups are most likely to benefit from treatment, or they could be used to track the progress of individual patients in treatment. In a randomized, controlled study with a form of medical food, de Waal et al used EEG to study the 2 groups.[101] The clustering coefficient and mean path length decreased in the control group but remained relatively unchanged in the treatment group. These results demonstrate the feasibility of graph analytical measures to track the effects of the disease and treatment over time. Future studies could yield graph analytical measures that determine if patients are suitable for or would benefit from treatment.

Conclusion

Graph analysis provides a useful way to measure and describe changes in network structure. The brain is a unique network that in optimal health exhibits efficiency in both local processing and global integration of information. Such properties are essential for cognition and can be accomplished through a small–world network. It follows that changes in network architecture may underlie cognitive dysfunction. It has been observed that AD causes widespread disconnection and alterations in brain network properties, particularly disrupting the small–world character. Functional and structural connectivity studies demonstrate randomization or regularization of brain networks in AD, and many of the changes correlate to decreases in cognition. While it has been shown that deviations of network properties occur with decreases in cognitive function, further study with graph analysis is needed to elucidate fully the nature and effect of network changes. Moreover, with advancements in technology and understanding, graph analysis potentially could be used to help diagnose and treat AD.

Acknowledgments

The author would like to thank JJG Geurts, MM Schoonheim, and AM Wink for their support and revision of an earlier version of this work.

References

    1. Alzheimer A. About a peculiar disease of the cerebral cortex. Allg Zeitschrift fur Psychiatr und Psychish–Gerichtlich Med. 1907;(64):146–148.return to text

    2. Tijms BM, Wink AM, de Haan W, et al. Alzheimer’s disease: connecting findings from graph theoretical studies of brain networks. Neurobiol Aging. 2013;34(8):2023–2036. doi:10.1016/j.neurobiolaging.2013.02.020.return to textreturn to text

    3. van den Heuvel MP, Hulshoff Pol HE. Exploring the brain network: a review on resting–state fMRI functional connectivity. Eur Neuropsychopharmacol. 2010;20(8):519–534. doi:10.1016/j.euroneuro.2010.03.008.return to textreturn to textreturn to text

    4. Sperling RA, Dickerson BC, Pihlajamaki M, et al. Functional alterations in memory networks in early Alzheimer’s disease. Neuromolecular Med. 2010;12(1):27–43. doi:10.1007/s12017–009–8109–7.Functional.return to text

    5. Mori S, van Zijl PCM. Fiber tracking: principles and strategies—a technical review. NMR Biomed. 15(7–8):468–480. doi:10.1002/nbm.781.return to text

    6. He Y, Chen ZJ, Evans AC. Small–world anatomical networks in the human brain revealed by cortical thickness from MRI. Cereb Cortex. 2007;17(10):2407–2419. doi:10.1093/cercor/bhl149.return to textreturn to text

    7. Tijms BM, Seriès P, Willshaw DJ, Lawrie SM. Similarity–based extraction of individual networks from gray matter MRI scans. Cereb Cortex. 2012;22(7):1530–1541. doi:10.1093/cercor/bhr221.return to text

    8. Bassett DS, Bullmore E, Verchinski BA, Mattay VS, Weinberger DR, Meyer–Lindenberg A. Hierarchical organization of human cortical networks in health and schizophrenia. J Neurosci. 2008;28(37):9239–9248. doi:10.1523/JNEUROSCI.1929–08.2008.return to textreturn to text

    9. Aertsen AM, Gerstein GL, Habib MK, Palm G. Dynamics of neuronal firing correlation: modulation of “effective connectivity.” J Neurophysiol. 1989;61(5):900–917. http://www.ncbi.nlm.nih.gov/pubmed/2723733. Accessed July 8, 2014.return to text

    10. Nunez PL, Srinivasan R, Westdorp AF, et al. EEG coherency. I: statistics, reference electrode, volume conduction, Laplacians, cortical imaging, and interpretation at multiple scales. Electroencephalogr Clin Neurophysiol. 1997;103(5):499–515. http://www.ncbi.nlm.nih.gov/pubmed/9402881. Accessed June 26, 2014.return to text

    11. Biswal B, Yetkin FZ, Haughton VM, Hyde JS. Functional connectivity in the motor cortex of resting human brain using echo–planar MRI. Magn Reson Med. 1995;34(4):537–541. http://www.ncbi.nlm.nih.gov/pubmed/8524021. Accessed May 26, 2014.

    12. Gross J, Kujala J, Hamalainen M, Timmermann L, Schnitzler A, Salmelin R. Dynamic imaging of coherent sources: studying neural interactions in the human brain. Proc Natl Acad Sci U S A. 2001;98(2):694–699. doi:10.1073/pnas.98.2.694.return to text

    13. Damoiseaux JS, Rombouts SARB, Barkhof F, et al. Consistent resting–state networks across healthy subjects. Proc Natl Acad Sci U S A. 2006;103(2): 13848–13853.return to text

    14. Gusnard DA, Raichle ME. Searching for a baseline: functional imaging and the resting human brain. Nat Rev Neurosci. 2001;2(10):685–694. doi:10.1038/35094500.return to text

    15. Greicius MD, Krasnow B, Reiss AL, Menon V. Functional connectivity in the resting brain: a network analysis of the default mode hypothesis. Proc Natl Acad Sci U S A. 2003;100(1):253–258. doi:10.1073/pnas.0135058100.return to text

    16. Mason MF, Norton MI, Van Horn JD, Wegner DM, Grafton ST, Macrae CN. Wandering minds: the default network and stimulus–independent thought. Science. 2007;315(5810):393–395. doi:10.1126/science.1131295.return to text

    17. Toussaint P-J, Maiz S, Coynel D, et al. Characteristics of the default mode functional connectivity in normal ageing and Alzheimer’s disease using resting state fMRI with a combined approach of entropy–based and graph theoretical measurements. Neuroimage. 2014;101:778–786. doi:10.1016/j.neuroimage.2014.08.003.return to textreturn to textreturn to text

    18. Metter EJ, Riege WH, Kameyama M, Kuhl DE, Phelps ME. Cerebral metabolic relationships for selected brain regions in Alzheimer’s, Huntington’s, and Parkinson’s diseases. J Cereb Blood Flow Metab. 1984;4(4):500–506. doi:10.1038/jcbfm.1984.74.return to text

    19. Freeman L. A set of measures of centrality based on betweenness. Sociometry. 1977;40(1):35–41.return to textreturn to text

    20. Watts DJ, Strogatz SH. Collective dynamics of “small–world” networks. Nature. 1998;393(6684):440–442. doi:10.1038/30918.return to text

    21. Newman MEJ. The structure and function of complex networks. 2003:58. Cornell University Library Web site. http://arxiv.org/abs/condmat/0303516. Accessed June 4, 2014.

    22. Latora V, Marchiori M. Efficient behavior of small–world networks. Phys Rev Lett. 2001;87(19):198701. doi:10.1103/PhysRevLett.87.198701.return to text

    23. Newman MEJ. Modularity and community structure in networks. Proc Natl Acad Sci U S A. 2006;103(23):8577–8582. doi:10.1073/pnas.0601602103.return to textreturn to textreturn to text

    24. de Haan W, van der Flier WM, Koene T, Smits LL, Scheltens P, Stam CJ. Disrupted modular brain dynamics reflect cognitive dysfunction in Alzheimer’s disease. Neuroimage. 2012;59:3085–3093. doi:10.1016/j.neuroimage.2011.11.055.return to textreturn to textreturn to text

    25. Stam CJ, Jones BF, Nolte G, Breakspear M, Scheltens P. Small–world networks and functional connectivity in Alzheimer’s disease. Cereb Cortex. 2007;17(1):92–99. doi:10.1093/cercor/bhj127.return to textreturn to textreturn to textreturn to text

    26. Stam CJ, de Haan W, Daffertshofer A, et al. Graph theoretical analysis of magnetoencephalographic functional connectivity in Alzheimer’s disease. Brain. 2009;132(Pt 1):213–224. doi:10.1093/brain/awn262.return to textreturn to textreturn to text

    27. Salvador R, Suckling J, Coleman MR, Pickard JD, Menon D, Bullmore E. Neurophysiological architecture of functional magnetic resonance images of human brain. Cereb Cortex. 2005;15(9):1332–1342. doi:10.1093/cercor/bhi016.return to text

    28. Sanabria–Diaz G, Martínez–Montes E, Melie–Garcia L. Glucose metabolism during resting state reveals abnormal brain networks organization in the Alzheimer’s disease and mild cognitive impairment. PLoS One. 2013;8(7):e68860. doi:10.1371/journal.pone.0068860.return to textreturn to textreturn to textreturn to text

    29. Hagmann P, Kurant M, Gigandet X, et al. Mapping human whole–brain structural networks with diffusion MRI. PLoS One. 2007;2(7):e597. doi:10.1371/journal.pone.0000597.return to textreturn to text

    30. He Y, Wang J, Wang L, et al. Uncovering intrinsic modular organization of spontaneous brain activity in humans. PLoS One. 2009;4(4):e5226. doi:10.1371/journal.pone.0005226.return to text

    31. Stam CJ, van Cappellen van Walsum AM, Micheloyannis S. Variability of EEG synchronization during a working memory task in healthy subjects. Int J Psychophysiol. 2002;46(1):53–66. http://www.ncbi.nlm.nih.gov/pubmed/12374646. Accessed June 8, 2014.return to text

    32. Gong G, He Y, Concha L, et al. Mapping anatomical connectivity patterns of human cerebral cortex using in vivo diffusion tensor imaging tractography. Cereb Cortex. 2009;19(3):524–536. doi:10.1093/cercor/bhn102.return to text

    33. Li Y, Liu Y, Li J, et al. Brain anatomical network and intelligence. PLoS Comput Biol. 2009;5(5):e1000395. doi:10.1371/journal.pcbi.1000395.return to text

    34. Zhu W, Wen W, He Y, Xia A, Anstey KJ, Sachdev P. Changing topological patterns in normal aging using large–scale structural networks. Neurobiol Aging. 2012;33(5):899–913. doi:10.1016/j.neurobiolaging.2010.06.022.return to textreturn to textreturn to text

    35. Wang L, Li Y, Metzak P, He Y, Woodward TS. Age–related changes in topological patterns of large–scale brain functional networks during memory encoding and recognition. Neuroimage. 2010;50(3):862–872. doi:10.1016/j.neuroimage.2010.01.044.return to textreturn to textreturn to textreturn to text

    36. Gong G, Rosa–Neto P, Carbonell F, Chen ZJ, He Y, Evans AC. Age–and gender–related differences in the cortical anatomical network. J Neurosci. 2009;29(50):15684–15693. doi:10.1523/JNEUROSCI.2308–09.2009.return to text

    37. Wu K, Taki Y, Sato K, et al. Age–related changes in topological organization of structural brain networks in healthy individuals. Hum Brain Mapp. 2012;33(3):552–568. doi:10.1002/hbm.21232.return to textreturn to text

    38. Achard S, Bullmore E. Efficiency and cost of economical brain functional networks. PLoS Comput Biol. 2007;3(2):e17. doi:10.1371/journal.pcbi.0030017.return to textreturn to text

    39. Chen ZJ, He Y, Rosa–Neto P, Gong G, Evans AC. Age–related alterations in the modular organization of structural cortical network by using cortical thickness from MRI. Neuroimage. 2011;56(1):235–245. doi:10.1016/j.neuroimage.2011.01.010.return to text

    40. Meunier D, Achard S, Morcom A, Bullmore E. Age–related changes in modular organization of human brain functional networks. Neuroimage. 2009;44(3):715–723. doi:10.1016/j.neuroimage.2008.09.062.return to text

    41. Kukull WA, Bowen JD. Dementia epidemiology. Med Clin North Am. 2002;86(3):573–590. http://www.ncbi.nlm.nih.gov/pubmed/12168560. Accessed July 1, 2014.return to text

    42. Saan R, Deelman B. De 15–Woordentest A en B. Groningen Afd Neuropsychol AZG. 1986. http://scholar.google.nl/scholar?hl=en&as_sdt=0,5&cluster=8983228692947986546#0. Accessed June 18, 2014.return to text

    43. Schmand B, Groenink SC, van den Dungen M. Letter fluency: psychometric properties and Dutch normative data [in Dutch]. Tijdschr Gerontol Geriatr. 2008;39(2):64–76. http://www.ncbi.nlm.nih.gov/pubmed/18500167. Accessed June 18, 2014.

    44. Lindeboom J, Matto D. Digit series and Knox cubes as concentration tests for elderly subjects [in Dutch]. Tijdschr Gerontol Geriatr. 1994;25(2):63–68. http://www.ncbi.nlm.nih.gov/pubmed/8197598. Accessed June 18, 2014.

    45. Smits LL, Pijnenburg YA, Koedam ELGE, et al. Early onset Alzheimer’s disease is associated with a distinct neuropsychological profile. J Alzheimers Dis. 2012;30(1):101–108. doi:10.3233/JAD–2012–111934.return to text

    46. Grundman M, Petersen RC, Ferris SH, et al. Mild cognitive impairment can be distinguished from Alzheimer disease and normal aging for clinical trials. Arch Neurol. 2004;61(1):59–66. doi:10.1001/archneur.61.1.59.return to text

    47. Selkoe DJ. Alzheimer’s disease results from the cerebral accumulation and cytotoxicity of amyloid beta–protein. J Alzheimers Dis. 2001;3(1):75–80. http://www.ncbi.nlm.nih.gov/pubmed/12214075. Accessed July 23, 2014.return to text

    48. Folstein MF, Folstein SE, McHugh PR. “Mini mental state”: a practical method for grading the cognitive state of patients for the clinician. J Psychiatr Res. 1975;12(3):189–198.return to text

    49. Delbeuck X, van der Linden M, Collette F. Alzheimer’s disease as a disconnection syndrome? Neuropsychol Rev. 2003;13(2):79–92.return to text

    50. Hagmann P, Cammoun L, Gigandet X, et al. Mapping the structural core of human cerebral cortex. PLoS Biol. 2008;6(7):e159. doi:10.1371/journal.pbio.0060159.return to text

    51. Minati L, Chan D, Mastropasqua C, et al. Widespread alterations in functional brain network architecture in amnestic mild cognitive impairment. J Alzheimers Dis. 2014;40(1):213–220. doi:10.3233/JAD–131766.return to text

    52. Greicius MD, Srivastava G, Reiss AL, Menon V. Default–mode network activity distinguishes Alzheimer’s disease from healthy aging: evidence from functional MRI. Proc Natl Acad Sci U S A. 2004;101(13):4637–4642. doi:10.1073/pnas.0308627101.return to textreturn to text

    53. de Haan W, Pijnenburg Y a., Strijers RL, et al. Functional neural network analysis in frontotemporal dementia and Alzheimer’s disease using EEG and graph theory. BMC Neurosci. 2009;10:101. doi:10.1186/1471–2202–10–101.return to textreturn to textreturn to textreturn to text

    54. Buckner RL, Sepulcre J, Talukdar T, et al. Cortical hubs revealed by intrinsic functional connectivity: mapping, assessment of stability, and relation to Alzheimer’s disease. J Neurosci. 2009;29(6):1860–1873. doi:10.1523/JNEUROSCI.5062–08.2009.return to text

    55. Sepulcre J, Sabuncu MR, Becker A, Sperling R, Johnson KA. In vivo characterization of the early states of the amyloid–beta network. Brain. 2013;136(Pt 7):2239–2252. doi:10.1093/brain/awt146.return to text

    56. Drzezga A, Becker JA, Van Dijk KRA, et al. Neuronal dysfunction and disconnection of cortical hubs in nondemented subjects with elevated amyloid burden. Brain. 2011;134(6):1635–1646. doi:10.1093/brain/awr066.return to text

    57. Stam CJ, van Cappellen van Walsum AM, Pijnenburg YAL, et al. Generalized synchronization of MEG recordings in Alzheimer’s disease: evidence for involvement of the gamma band. J Clin Neurophysiol. 2002;19(6):562–574. doi:10.1097/00004691–200212000–00010.return to text

    58. Tahaei MS, Jalili M, Knyazeva MG. Synchronizability of EEG–based functional networks in early Alzheimer’s disease. IEEE Trans Neural Syst Rehabil Eng. 2012;20(5):636–641. doi:10.1109/TNSRE.2012.2202127.return to text

    59. Stam CJ, Jones BF, Manshanden I, et al. Magnetoencephalographic evaluation of resting–state functional connectivity in Alzheimer’s disease. Neuroimage. 2006;32(3):1335–1344. doi:10.1016/j.neuroimage.2006.05.033.return to textreturn to text

    60. Wang K, Liang M, Wang L, et al. Altered functional connectivity in early Alzheimer’s disease: a resting–state fMRI study. Hum Brain Mapp. 2007;28(10):967–978. doi:10.1002/hbm.20324.return to text

    61. Chen G, Zhang H-Y, Xie C, et al. Modular reorganization of brain resting state networks and its independent validation in Alzheimer’s disease patients. Front Hum Neurosci. 2013;7(August):456. doi:10.3389/fnhum.2013.00456.return to text

    62. Liu Z, Zhang Y, Bai L, et al. Investigation of the effective connectivity of resting state networks in Alzheimer’s disease: a functional MRI study combining independent components analysis and multivariate Granger causality analysis. NMR Biomed. 2012;25(12):1311–1320. doi:10.1002/nbm.2803.return to text

    63. Rombouts SA, Barkhof F, Goekoop R, Stam CJ, Scheltens P. Altered resting state networks in mild cognitive impairment and mild Alzheimer’s disease: an fMRI study. Hum Brain Mapp. 2005;26(4):231–239. doi:10.1002/hbm.20160.return to text

    64. Binnewijzend MA, Schoonheim MM, Sanz–Arigita E, et al. Resting–state fMRI changes in Alzheimer’s disease and mild cognitive impairment. Neurobiol Aging. 2012;33(9):2018–2028. doi:10.1016/j.neurobiolaging.2011.07.003.return to text

    65. de Haan W, Stam CJ, Jones BF, Zuiderwijk IM, van Dijk BW, Scheltens P. Resting–state oscillatory brain dynamics in Alzheimer disease. J Clin Neurophysiol. 2008;25(4):187–193. doi:10.1097/WNP.0b013e31817da184.return to text

    66. Stam CJ, van Dijk BW. Synchronization likelihood: an unbiased measure of generalized synchronization in multivariate data sets. Phys D Nonlinear Phenom. 2002;163(3–4):236–251. doi:10.1016/S0167–2789(01)00386–4.return to text

    67. Vecchio F, Miraglia F, Curcio G, et al. Cortical brain connectivity evaluated by graph theory in dementia: a correlation study between functional and structural data. J Alzheimers Dis. 2015;45:745–756. doi:10.3233/JAD–142484.return to textreturn to text

    68. Brett M, Johnsrude IS, Owen AM. The problem of functional localization in the human brain. Nat Rev Neurosci. 2002;3(3):243–249. doi:10.1038/nrn756.return to text

    69. Vecchio F, Miraglia F, Marra C, et al. Human brain networks in cognitive decline: a graph theoretical analysis of cortical connectivity from EEG data. J Alzheimers Dis. 2014;41(1):113–127. doi:10.3233/JAD–132087.return to text

    70. Montez T, Linkenkaer–Hansen K, van Dijk BW, Stam CJ. Synchronization likelihood with explicit time–frequency priors. Neuroimage. 2006;33(4):1117–1125. doi:10.1016/j.neuroimage.2006.06.066.return to text

    71. Supekar K, Menon V, Rubin D, Musen M. Network analysis of intrinsic functional brain connectivity in Alzheimer’s disease. PLoS Comput Biol. 2008;4(6):e1000100. doi:10.1371/journal.pcbi.1000100.return to textreturn to textreturn to textreturn to textreturn to text

    72. Tzourio–Mazoyer N, Landeau B, Papathanassiou D, et al. Automated anatomical labeling of activations in SPM using a macroscopic anatomical parcellation of the MNI MRI single–subject brain. Neuroimage. 2002;15(1):273–289. doi:10.1006/nimg.2001.0978.return to text

    73. Percival DB, Walden AT. Wavelet Methods for Time Series Analysis. Cambridge: Cambridge University Press; 2006. http://books.google.com/books?id=UqUi2NviqFcC&pgis=1. Accessed July 7, 2014.return to text

    74. Sanz–Arigita E, Schoonheim MM, Damoiseaux J, et al. Loss of “small–world” networks in Alzheimer’s disease: graph analysis of fMRI resting–state functional connectivity. PLoS One. 2010;5(11):e13788. doi:10.1371/journal.pone.0013788.return to textreturn to textreturn to text

    75. Zhao X, Liu Y, Wang X, et al. Disrupted small–world brain networks in moderate Alzheimer’s disease: a resting–state fMRI study. PLoS One. 2012;7(3):e33540. doi:10.1371/journal.pone.0033540.return to textreturn to textreturn to textreturn to text

    76. Kim H, Yoo K, Na DL, Seo SW, Jeong J, Jeong Y. Non–monotonic reorganization of brain networks with Alzheimer’s disease progression. Front Aging Neurosci. 2015;7(June):1–10. doi:10.3389/fnagi.2015.00111.return to textreturn to textreturn to textreturn to text

    77. Berg L. Clinical dementia rating. Br J Psychiatry. 1984;145:339. http://www.ncbi.nlm.nih.gov/pubmed/6478132. Accessed July 23, 2014.return to text

    78. Sohn WS, Yoo K, Na DL, Jeong Y. Progressive changes in hippocampal resting–state connectivity across cognitive impairment: a cross–sectional study from normal to Alzheimer disease. Alzheimer Dis Assoc Disord. 2014;28(3):239–246. doi:10.1097/WAD.0000000000000027.return to text

    79. Ciftçi K. Minimum spanning tree reflects the alterations of the default mode network during Alzheimer’s disease. Ann Biomed Eng. 2011;39(5):1493–504. doi:10.1007/s10439–011–0258–9.return to textreturn to text

    80. Bellec P, Rosa–Neto P, Lyttelton OC, Benali H, Evans AC. Multi–level bootstrap analysis of stable clusters in resting–state fMRI. Neuroimage. 2010;51(3):1126–1139. doi:10.1016/j.neuroimage.2010.02.082.return to text

    81. Seo EH, Lee DY, Lee JM, et al. Whole–brain functional networks in cognitively normal, mild cognitive impairment, and Alzheimer’s disease. PLoS One. 2013;8(1):e53922. doi:10.1371/journal.pone.0053922.return to textreturn to textreturn to text

    82. Lo C-Y, Wang P-N, Chou K-H, Wang J, He Y, Lin C-P. Diffusion tensor tractography reveals abnormal topological organization in structural cortical networks in Alzheimer’s disease. J Neurosci. 2010;30(50):16876–16885. doi:10.1523/JNEUROSCI.4136–10.2010.return to textreturn to text

    83. He Y, Chen Z, Evans A. Structural insights into aberrant topological patterns of large–scale cortical networks in Alzheimer’s disease. J Neurosci. 2008;28(18):4756–4766. doi:10.1523/JNEUROSCI.0141–08.2008.return to textreturn to textreturn to text

    84. Li Y, Wang Y, Wu G, et al. Discriminant analysis of longitudinal cortical thickness changes in Alzheimer’s disease using dynamic and network features. Neurobiol Aging. 2012;33(2):427.e15–30. doi:10.1016/j.neurobiolaging.2010.11.008.return to textreturn to text

    85. Phillips DJ, McGlaughlin A, Ruth D, Jager LR, Soldan A. Graph theoretic analysis of structural connectivity across the spectrum of Alzheimer’s disease: the importance of graph creation methods. NeuroImage Clin. 2015;7:377–390. doi:10.1016/j.nicl.2015.01.007.return to textreturn to textreturn to text

    86. Yao Z, Zhang Y, Lin L, Zhou Y, Xu C, Jiang T. Abnormal cortical networks in mild cognitive impairment and Alzheimer’s disease. PLoS Comput Biol. 2010;6(11):e1001006. doi:10.1371/journal.pcbi.1001006.return to textreturn to textreturn to text

    87. Tijms BM, Mueller C, Vrenken H, et al. Single–subject grey matter graphs in Alzheimer’s disease. PLoS One. 2013;8(3):e58921. doi:10.1371/journal.pone.0058921.return to textreturn to text

    88. Carmeli C, Fornari E, Jalili M, Meuli R, Knyazeva MG. Structural covariance of superficial White matter in mild Alzheimer’s disease compared to normal aging. Brain Behav. 2014;4(5):721–737. doi:10.1002/brb3.252.return to textreturn to text

    89. Fornari E, Maeder P, Meuli R, Ghika J, Knyazeva MG. Demyelination of superficial white matter in early Alzheimer’s disease: a magnetization transfer imaging study. Neurobiol Aging. 2012;33(2):428.e7–428.e19. doi:10.1016/j.neurobiolaging.2010.11.014.return to text

    90. Pineda–Pardo JA, Garcés P, López ME, et al. White matter damage disorganizes brain functional networks in amnestic mild cognitive impairment. Brain Connect. 2014;4(5):312–322. doi:10.1089/brain.2013.0208.return to text

    91. Hayasaka S, Laurienti PJ. Comparison of characteristics between region–and voxel–based network analyses in resting–state fMRI data. Neuroimage. 2010;50(2):499–508. doi:10.1016/j.neuroimage.2009.12.051.return to textreturn to text

    92. Schmidt C, Redyk K, Meissner B, et al. Clinical features of rapidly progressive Alzheimer’s disease. Dement Geriatr Cogn Disord. 2010;29(4):371–378. doi:10.1159/000278692.return to text

    93. Tijms BM, Yeung HM, Sikkes SAM, et al. Single–subject gray matter graph properties and their relationship with cognitive impairment in early– and late–onset Alzheimer’s disease. Brain Connect. 2014;4(5):337–346. doi:10.1089/brain.2013.0209.return to text

    94. Shu N, Liang Y, Li H, et al. Disrupted topological organization in white matter structural networks in amnestic mild cognitive impairment: relationship to subtype. Radiology. 2012;265(2). doi:10.1148/radiol.12112361/–/DC1.return to text

    95. Brier MR, Thomas JB, Fagan AM, et al. Functional connectivity and graph theory in preclinical Alzheimer’s disease. Neurobiol Aging. 2014;35:757–768. doi:10.1016/j.neurobiolaging.2013.10.081.return to text

    96. Li J, Jin Y, Shi Y, et al. Voxelwise spectral diffusional connectivity and its applications to Alzheimer’s disease and intelligence prediction. Med Image Comput Comput Assist Interv. 2013;16(Pt 1):655–662.return to text

    97. Daianu M, Jahanshad N, Nir TM, et al. Breakdown of brain connectivity between normal aging and Alzheimer’s disease: a structural k-core network analysis. Brain Connect. 2013;3(4):407–422. doi:10.1089/brain.2012.0137.return to text

    98. Ahmadlou M, Adeli H, Adeli A. New diagnostic EEG markers of the Alzheimer’s disease using visibility graph. J Neural Transm. 2010;117(9):1099–109. doi:10.1007/s00702–010–0450–3.return to text

    99. Khazaee A, Ebrahimzadeh A, Babajani–Feremi A. Identifying patients with Alzheimer’s disease using resting–state fMRI and graph theory. Clin Neurophysiol. 2015;126(11):2132–2141. doi:10.1016/j.clinph.2015.02.060.return to text

    100. Khazaee A, Ebrahimzadeh A, Babajani–Feremi A. Application of advanced machine learning methods on resting–state fMRI network for identification of mild cognitive impairment and Alzheimer’s disease. Brain Imaging Behav. September 12, 2015. doi:10.1007/s11682–015–9448–7.return to text

    101. de Waal H, Stam CJ, Lansbergen MM, et al. The effect of souvenaid on functional brain network organisation in patients with mild Alzheimer’s disease: a randomised controlled study. PLoS One. 2014;9(1):e86558. doi:10.1371/journal.pone.0086558.return to text