From Models-as-Fictions to Models-as-Tools

Abstract

Many accounts of scientific modeling conceive of models as fictions: there are analogies between models and various aesthetic objects, as well as between how scientists interact with models and how authors interact with fictions. Fictionalists, like most accounts of models, take models to be revelatory of the actual world in virtue of bearing some resemblance relation to a target system. While such fictionalist accounts capture crucial aspects of modelling practice, they are ill-suited to some design and engineering contexts. Here, models sometimes serve to underwrite design projects whereby real-world targets are constructed. In such circumstances, it is unclear what the model is supposed to resemble. Further, while fictionalists often require that models qua models have their content in virtue of construal or interpretation, in some engineering and design contexts success-conditions do not require such content—all that is required is that the model generates the required outputs. I take these points to motivate a view which accommodates fictionalism, but is broader. I articulate and defend an account of models as tools: specifically, material objects which are put to particular uses in particular contexts.

1. Introduction

Fictionalism about scientific models captures crucial insights about the often rich, sophisticated content of models and how modellers interact with them. However, I’ll argue that such accounts fall short of handling some of the dynamic, world-directed purposes that models serve in engineering and design. In brief, fictionalism requires that the world-directed success of models turns on their adequately representing some target system. However, engineering models often serve as scaffolds for the construction of real-world systems as well as further models. As such, their success doesn’t turn on their representing target systems, or further fictional systems, as fictionalists require. In such cases there is no resemblance between a model and a pre-existing part of the world because the model is involved in constructing that system and, during engineering and design, there is a dynamic relationship between the two. Further, I’ll argue that some of the uses models are put to do not require that they be understood as fictions. On my view, this motivates a more pragmatic account of modeling, one which takes models to be tools: material objects which are put to some use. I’m not the first to suggest an account like this (see, in particular, Boumans 2012; Knuuttila 2011); however, previous work has lacked both precision—an account of what a tool is—and an explanation of how it captures the insights of fictionalism. In what follows I’ll tackle both. I’ll start with an example of the kind of modelling we’re concerned with. I’ll then discuss fictionalist views and argue that they cannot accommodate such models, before turning to my positive account.

2. Models in Design

My father is a hydraulics engineer, primarily busy with designing, and monitoring the construction and functioning of, large pumps for extracting water from artesian wells. In so doing, he interacts with a number of more or less idealized theoretical objects—models. These aid him by being simplified, easily tractable, and manipulable proxies.

The process of selecting a pump comes in three stages. First, a location is selected for the future pump and a well is drilled. Water is drawn from the well in order to calculate the draw-down curve. This tells us how much the aquifer’s ‘head’ (the top of the water) will descend as water is pumped.

Second, we reach a proxy stage. The draw-down curve and the project’s requirements are used in combination with some fairly simple models to work out how much water, at what rate, could be drawn from the well and how much power would be required in doing so. One such model is the mass-flow equation, which treats pipe friction pressure as proportional to the square of the flow. That is, as water flow increases, the amount of friction pressure from the pipe increases exponentially. This is important for understanding the pressure the pump will need to overcome, and the amount of ‘suction’ required to lift water from the well into its new location (a storage tank, for instance). For a particular design scenario, further details are added, leading to equations like the following:

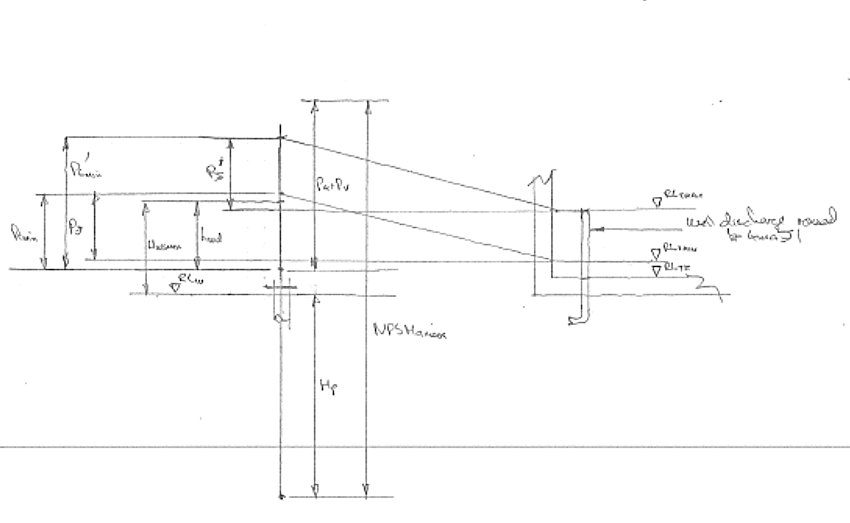
Ptmax is the maximal pump pressure required to lift the water to the delivery pipe discharge in the storage tank. This value matters for the next stage, when we select our pump. Variable Hwd is the well draw-down amount at flow Q. This was the value established in the first stage. The pressure the pump must produce is dependent on variable Hwsmin, the minimal level of the well over summer; constant Hd, the distance between the tank’s floor and the height of the delivery pipe’s discharge; and variable Pd, the pipe friction loss at flow Q (which is determined by the mass-flow equation). By determining Ptmax, a system curve is generated which provides a profile of the capacities of a pump which would manage maximal well capacity. However, this model is only preliminary: it does not provide the minimal pump pressure required to lift the water to the delivery pipe discharge in the storage tank, and it assumes a particular type of pipe and its characteristic friction coefficient. The actual capacity depends on atmospheric and water vapour pressure, specific characteristics of the well, and seasonal well level variations. With some of these details added, further models generate hydraulic curves (which map total head against flow volume) for that particular scenario. Which is to say, curves for that particular well, particular delivery pipe and particular storage tank. Although it is technically unnecessary, my father often draws schematic hydraulic line diagrams to aid in his understanding and imagining of the future pump:

Figure 1. Hydraulic Line Diagram. (by Mike Currie)

In the third stage, a computer program selects the optimal pump design given the requirements of the calculations: one which can handle both the minimal and maximal pressures, and those in between. This is, in effect, carried out by comparing the hydraulic curves from step two to the performance curves of various pumps. That which most efficiently meets the requirements is selected and ordered.

In short, in pump selection my father interacts with the actual well site at the initial stage—determining the well draw-down curve. Otherwise, he utilizes proxies: simple, theoretical models, schematic diagrams, imagined content, and geometric curves.

A fictionalist about models takes my father to be interacting with these proxies similarly to how he interacts with the high-fantasy novels he enjoys.[1] That is, models have fictional content: they are representational as literary fiction is. Although some of the time—quite often—a modeller does treat her model in fictional terms, such views do not capture some of the proxies used by my father in pump selection. Fictionalists (and others, of course) take models to inform us about the world in virtue of there being some kind of resemblance relation between the model and the target system. However, the effectiveness of the model utilized in the second stage above doesn’t turn on its resembling the real world: it is intended to scaffold further model construction. More crucially, although the model is directed towards the pump and the well site, there isn’t an instantiated target system per se: after all, the well hasn’t been built yet. Second, the use of models in the third stage doesn’t require a fictional relationship: my father simply must be convinced that the required inputs will generate the required outputs.

None of this suggests that fictionalism doesn’t account for many aspects of modeling practice. Rather, it suggests that fictionalism about models must be supplemented, or, by my account, subsumed into a larger framework. As Adam Toon has said, “the real test of fiction-based approaches must be whether they can provide a coherent overall account of scientific modeling” (2011: 580). I do not question fictionalism’s coherence, but its completeness. Instead of viewing fictionalism as a full account of models, then, we should take it as one aspect of a broader set of activities. I’ll argue that a tool-based view can account for both fictionalism and that broader set.

3. Three Questions about Theoretical Models.

Right out of the gate, it’s important to note an ambiguity about philosophical appeals to fictionalism regarding models. That is, ‘fictionalism’ can be understood in two different ways, which are logically independent. On one hand, fictionalism is contrasted with realism; realists take models to provide literally true descriptions of the world, fictionalists take them to be descriptions of fictions—they disagree over the referent of model content. On the other hand, we can contrast fictionalists with structuralists. For a structuralist, the representational capacity of models is restricted to the formal and the mathematical; models describe trajectories through state spaces, relationships between variables, and geometric properties. Fictionalists take the content of models to be richer: models carry concrete content. For the structuralist, the mass-flow equation expresses a linear relationship between two variables, while the fictionalist claims that it expresses two physical qualities, properties or forces and their interaction.

So, the first fictionalist is interested in the referent of model content; the second is interested in the nature and expressive power of models. Although these are related, I will only be concerned with the latter view in this paper.

For my purposes, fictionalists target three main questions about models (cf. Frigg 2010). Let’s call the first the semantic question: when are claims about models true? When my father says, for example, “pipe friction pressure is exponentially proportional to flow”, according to what rules is the statement true or false? For the fictionalist, this question is analogous to enquiring after claims internal to fictions such as “The little prince lived on a small planet”.

Answers to the semantic question constrain, but do not decide, answers to the second question: the metaphysical question. Here, we ask what a model is—you might say, we ask after the truth-makers of claims about models. Often fictionalists are motivated by deflationism about the metaphysical question: insofar as they can, they try to minimize the metaphysical commitments required by their view. Prima facie, stipulating fictional possibilia brings metaphysical costs, which fictionalists typically seek to avoid (Levy 2012; Thomson-Jones 2010; Toon 2012).

Finally, fictionalists try to answer the model-world question. Scientific models have epistemic powers, they are taken to inform us about the real world—even as they diverge dramatically from being accurate descriptions of it. In virtue of what can they do this?

In the next section I sketch how fictionalists answer the semantic, metaphysical, and model-world questions, which sets us up for the objections in Section 5, and will be important for demonstrating how a tool-based view can accommodate fictionalism in Section 6.

4. Fictionalism about Models

As we saw above, a basic motivation behind fictionalism is a commitment to a concrete as opposed to an abstract (or structural) view of models. To begin, distinguish between a model’s content and its vehicle. A model’s content is what it expresses. The mass-flow equation, for instance, expresses a relationship between two variables: friction and flow. It tells us that as flow increases, friction increases exponentially. A model’s vehicle is the object which ‘carries’ that content—its medium. A hydraulic line diagram is a vehicle which in part expresses the mass-flow model’s content. An abstract view of models claims that a model’s content is exhausted by structural or relational features (see, e.g., Giere 1988; Suarez 2003; Weisberg 2013).[2] In effect, a model says only mathematical things. According to fictionalists, taking models as abstracta in this sense is too thin: many models do not seem to have mathematical content, or mathematical content alone. This is clear enough in some cases: when my father runs a mental simulation of water running through a pump, or builds a scale model, or sketches a hydraulic line diagram, it is hard to see how we could understand such models as abstracta. They seem to express concrete content. In theoretical cases, too, the content of a model appears to outrun mere structure. The mass-flow equation, for instance, seems to express facts about pipe pressure—not merely variables. Moreover, it is somewhat unclear how we are to compare the abstract properties of models—variables, state-spaces, and so on—to the world’s concrete properties. And indeed, when models do say things about the world, they do not appear to do this in a straight-forward way. It is not literally true that the water in a pumping station acts as my father’s model represents it: factors such as variation in well levels also affect pump pressure. There is no simple mapping between abstract properties and concrete properties[3] (see Frigg 2010; Levy 2015; and Thomson-Jones 2010 for more detailed treatments). Moreover, mere structural properties don’t do justice to the manipulability and physicality of models in virtue of which they enable such dynamic interactions with modellers themselves (Knuuttila 2011). Finally, Fiora Salis (2016) has recently argued that sophisticated structuralist accounts such as Weisberg’s ultimately rely on fictionalist content after all.[4] If she is right, then my arguments should straightforwardly apply in those contexts as well.

By taking models as concrete, model-to-world relations can be understood as comparisons between (or descriptions of) concrete properties. Moreover, the non-mathematical features of models are easily accommodated. A further motivation is the ‘face value practice’ (Thomson-Jones 2010) of modeling: undoubtedly scientists discuss and interact with models in a way which makes fictionalism attractive (see Godfrey-Smith 2009; Toon 2011; Weisberg 2013: Chapter 4).

However, appealing to models as expressing or possessing concrete properties doesn’t get us far in answering the questions posed above. To fill out their views, fictionalists appeal to positions developed in aesthetics. In effect, taking models as fictions provides a conduit for applying conceptual machinery about fictions to models. This allows philosophers to attempt the tightrope between staying true to modeling practice while avoiding costly metaphysical commitments. The most promising attempts at this trick co-opt Kendall Walton’s (1990) view of fiction. I’ll focus on these, but it’s important to note that I intend the objections in the next section to apply to any fictionalist account—or for that matter, any account of modelling generally—which requires a resemblance relation between a model and a target system, and which puts strong enough emphasis on the imagination for successful model uses.

A way into the philosophy of fiction is via notions of fictional truth. In virtue of what is it true, say, that “The Little Prince lived on a very small planet (perhaps B-612) with three volcanoes, two extinct and one active”? How can it be true when the actual world has never contained a little prince living on a very small planet? The answer is to take the above sentence to refer to some fictional, rather than the actual, world. It could be paraphrased as, “according to Antoine de Saint-Exupéry’s story, the Little Prince lived on a very small planet (and so on …)”. So, fictions have ‘internal’ truths, propositions which are true according to the fiction. The challenge is working out where these internal truths come from. One could take fictions to refer to sets of possibilia: “the Little Prince lived on a very small planet” is true just in case, across the set of possible worlds which cohere with what is said in Saint-Exupéry’s story, that sentence is true. This has nice semantic features, but is rather problematic metaphysically speaking (see, e.g., Thomasson 1999: Chapter 1). What do we take these possibilia to be? Positing a real, concrete group of physical Princes meeting Saint-Exupéry’s description is metaphysically rash. Moreover, presumably the author of the work isn’t merely describing possibilia; Saint-Exupéry created his characters.

The trick in the metaphysics of fiction, then, is to capture a notion of ‘internal’, or ‘fictional’ truth, while so far as possible limiting one’s metaphysical commitments and keeping in tune with the actual practices of creating and consuming literature.

Kendall Walton’s (1990) approach is to take fictions as games of make-believe.[5] Such games are facilitated by props: material objects which, in combination with various ‘rules of generation’ demand that players imagine certain propositions as true. Children playing lava use material objects—furniture and the floor—as props. According to the game, the floor is ‘lava’, while the furniture is safe. The claim ‘Eloise fell into the lava, she is dead’ is true, according to the game of make-believe, just in case Eloise touched the floor. The rules of the game and the props prescribe such an act of imagining. Claims in literary fictions work similarly: the various realizers of Saint-Exupéry’s story—books, performances, and so forth—are props which, in combination with some set of rules, demand that people consuming the fiction imagine such-and-such to be the case.

It is important to note that Walton’s view involves a special notion of ‘representation’. Contrast a broad sense of representation with Walton’s more narrow conception. Broadly speaking, in order to represent, an object must have propositional content. For it to be a representation of another object, that content must be ‘about’ that object. By contrast, in Walton’s usage, something represents just in case it is a prop in a game of make-believe. This is a narrower usage; for Walton ‘represent’ is a term of art. The semantic question asks how models represent in the context of fiction, the model-world question asks how models might be about the world. As we’ll see, although Walton-style fictionalism provides a compelling answer to the former question in some contexts (but not all), it must be supplemented to answer the latter question. In the next section, I’ll complain about both the requirement that models are representational in Walton’s sense, and about the supplements that have been attempted to answer the model-world question.

So, Walton’s view looks ripe for co-opting by those concerned with the metaphysics of models (Levy 2015; Frigg 2010; and Toon 2012 are prominent examples). The mechanics of truths about models can be straightforwardly transferred. Modellers interact with various props—say, inscriptions of equations, or computer software, or perhaps the model’s target itself—and these encourage acts of imagining, thus generating internal truths. The props are the model’s vehicle (or alternatively the part of the world the model targets), and internal truths are generated by the games such vehicles prescribe. This answers the semantic question. But this doesn’t tell us how it is that models say true things of the world: the model-world question. Similarly, The Little Prince is a partly allegorical work—from reading it, we are supposed to learn about the nature of, say, adulthood in the actual world. The world of adults in The Little Prince is absurd, and this absurdity is reflected in our own world. We can categorize fictionalists by how they characterize this mode of theorizing. First, indirect accounts take the model-world relationship to be mediated by some further object—the model. Second, by direct accounts the model is, in some sense, a description: there is no mediation.

To see the difference between direct and indirect views, a tripartite distinction first drawn by Ron Giere (1988) will be helpful (see also Godfrey-Smith 2006). On this picture, we should distinguish between model descriptions, model systems, and target systems. The model system is whatever it is that modellers directly examine. It is, in Godfrey-Smith’s terms, whatever is “analyzed, described and argued about” (2009: 102) in modeling. Answering the metaphysical question involves an account of model systems. Model descriptions specify model systems: they could be a set of equations (perhaps written down, carried in someone’s head, or realized on a computer), an image, a material object, or whatever (I assume we can equate a model description with its vehicle). A target system is the part of the world we take the model to be informative about. My father might specify a model system using a mass-flow equation, and take this to inform him about his target system, a pump.

For indirect fictionalists, most well realized by Roman Frigg and collaborators (Frigg 2010; Frigg & Nguyen 2016), but also discussed by Peter Godfrey-Smith (2009), the model-world question is achieved through property comparisons:

The fiction somehow licences, ‘puts on the table’, the relevant fictional properties, and thus comparisons between them and actual properties. We might ask whether shifting the metaphysical burden from abstract objects to uninstantiated properties is less metaphysically onerous (Levy 2015). More problematically, it is not obvious how comparisons between instantiated and uninstantiated properties can yield truths about the world (Godfrey-Smith 2009; Salis 2016).[6] Although Frigg and Nguyen provide an expanded indirect account, they do not specify how the model-world connection is made, as “This question has no straightforward answer and much depends on one’s ontological commitments” (2016: 239). Even with a good story of property-comparisons in hand, this won’t avoid my objections in Section 5, which turn on modeling’s requiring an explicit comparison between some model system and some target system.

Direct fictionalists aim for a cleaner metaphysical plate. Both approaches agree that internal claims about models work according to Walton’s machinery. However, they differ on the metaphysics and model-world question. Where indirect fictionalists take a model system to be a game of make-believe, direct fictionalists, in a sense, deny there is a model system at all.

Direct fictionalists suggest we take model systems to be descriptions of target systems.[7] On this view, a model is more like a metaphor than a fiction: we describe our target in a way which emphasizes some aspects over others.

This suggestion overturns the idea that models are indirect representations of target systems. The immediate advantage is the avoidance of comparing either nonexistent fictional entities or nonexistent fictional properties with the existing world. There is simply the world and our interaction with it. This answers the metaphysical question, and internal truths are generated as they are for indirect fictionalists—via the props and rules of generation.[8]

Arnon Levy (2015) explicitly targets the model-world question. The model just is a description of the world; the props are identified with the target system. However, the model is still a false description of the world: and so, how should we understand the model-world relation? Levy takes the relation to be one of partial truth. Roughly, the notion of partial truth involves parceling up propositions or sentences into components, which are themselves true or false (see Yablo 2014). So, the content of complex sentences can be understood as consisting in several parts, each with their own truth conditions. As opposed to conceiving of ‘truth’ as ranging over full sentences, it ranges over these sentence parts. A sentence is ‘partially true’ when at least one of its parts is true. Let’s take a fictional example, considering Romeo in act 2, scene 2:

The last sentence is, of course, false—even in the fiction: Juliet is a 13 year old human female, not a star. However, we could very roughly understand the sentence as composed of two parts: “Juliet is at the eastern window” and “Juliet is the sun”. Naturally, it loses something in the translation, but I take it that according to Shakespeare’s fiction, the former sentence is true and the latter is false. The metaphor, then, could be understood as being partially true in Yablo’s sense. Similarly, Levy suggests that we partition the false and true aspects of the model’s content in virtue of which it says something true (when it does!) about its target system. On this kind of view, we should take my father’s model pump to be a description of the actual pump—perhaps something akin to its blueprints, or a map. Aspects of a map’s representational content are true and aspects are false. A map gets it right when it gets it right in the relevant respects. Models are direct, rather than indirect, representations.

The purpose of going into this amount of detail about fictionalist views is two-fold. First, it is important to see that the two objections I provide in Section 5 are not solved by the kinds of precisifications attempted by Levy, Frigg, and company. These all turn on (1) there being a more or less explicit resemblance relationship between the model (or description) and some target system, and (2) models-qua-models necessarily demanding certain acts of imagining on the modeller’s part. On my view, both commitments are problematic in engineering or design contexts. Second, my aim in Section 6 is to encompass the successful parts of fictionalism into a broader account, and seeing how this operates requires a firm grounding in varieties of fictionalism.

5. Fictionalism and Design

In what follows, I do not deny that models are representational in a broad sense, that they are ‘about’ target systems and function as proxies. Rather, I deny that this aboutness is captured in fictionalist terms. First, both direct and indirect fictionalists answer the model-world question in terms of there being some resemblance between a model and a fixed target system. For Frigg, this is a property-comparison; for Levy, a relation of partial truth. But there are world-directed uses of models where their purpose is to scaffold both further models and the construction of ‘target’ systems themselves. As such, there seems to be no good target for the property comparison or the truth-relation, and moreover the success of the model explicitly doesn’t rely on those kinds of factors. Second, for fictionalists, being a Walton-style representation is essential to modeling. But models are not representational in the same way that fictions are. That is, they are not essentially representational. Stripped of representational content, a literary fiction is no fiction. That is to say, it is plausible that possessing fictional representational content is a necessary condition for something to count as a fiction. However, models may be—in fact often are—stripped of such content. Fictions qua fictions—as opposed to, say, inscriptions, or mistaken non-fictional reports, are always (Walton-style) representations. Models qua models are not. As I’ll make explicit, both problem cases arise in the modelling work I described at the paper’s beginning.

Philosophers considering models often speak as if, when considering the model-world relation, there are two kinds of models: ‘general’ models which in some sense lack targets (although see Levy 2015), and what Weisberg (2013) calls ‘targeted models’, those concerned with representing a particular system. However, the use of models to scaffold further model construction, and to design and construct physical systems, represent a third class which, I’ll now argue, fictionalists cannot account for.

During the pump selection process my father will often utilize models whose features are geared towards the specific site, and the particular pump he intends to select, so they are not general or targetless models. Determining pump suction requires taking atmospheric pressure into account, and as atmospheric pressure changes both with altitude, the position of the pump, and the depth of the well, these factors make specific differences to how we model the pump. However, the pump has not been selected as yet: the specific target appears to lack an extension. What, then, does the model describe or represent? Presumably either a future object (the pumping station that will be built) or some kind of nonexistent object (the pumping station intended to be built). What do these cases look like on fictionalist views? On an indirect view we are, presumably, comparing abstract properties to either future properties or further abstract properties. But these future properties are either indeterminate (depending on how the world turns out), or our epistemic access to them is mysterious.

On direct views, it is unclear what we should take the props to be. They could be, for instance, the well site—the object concurrent with the selection process. Alternatively, they could be the future object—the completed pump. Perhaps we should view the model as a prediction about the future state; the model describes a future object. However, we cannot take these models to be in the business of predicting future states. This is because they are preliminary: they are a way of getting the selection process off the ground. These early designs and models are often abandoned, functioning as scaffolding for yet more detailed models. Such preliminary models typically succeed in their task: forming a basis for further design, necessary for the final product. The journey from an initial proposal to a complete pumping station is a long one, each step frequently involving the mediation of various proxies—and their abandonment. This suggests that thinking of models in terms of partial truths or property comparison is insufficient to capture the use of models: frequently, an explicit resemblance relation between model and world doesn’t enter into it.

So, fictionalist construals of modeling answer the model-world question by positing a kind of relationship between the fictional content of the model and the nature of the target system. In engineering cases, the model’s target is in some sense unspecified—the target is perhaps an indeterminate fictional object, or an object in the future. However, the success of the model’s world-directed task is not to be partially true of the future object, nor to promote property comparisons between two fictional objects. Rather, the function of the model is to scaffold the construction of models which themselves are used for pump construction or selection. Moreover, there is often a dynamic relationship between models and targets in design contexts. Which pump we select, and the properties of the eventual pumping station, are not simply decided by the ‘final’ model, rather, the model—and the physical properties of the pump—are often updated in virtue of ongoing changes in context.

A further objection to the idea that fictionalist accounts can provide a general, complete account of modeling practice arises from considering the models used in the last stage of pump-selection. This objection hits the use of Walton’s specific sense of ‘representation’: that to represent, a fiction must be a prop in a game of make-believe. That is, for models to be models they must demand certain acts of imagining. Recall that the mass-flow equation, when taken as a veridical description of the world is, strictly speaking, false. There are two possible senses of ‘false’ here. First, the equation represents pipe friction as if it were not affected by, say, atmospheric pressure—it is non-veridical in a way similar to how the floor in a game of lava is not hot. Second, the output of the equation will be inexact: it will not predict pipe friction in a fine-grained way. Michael Weisberg (2007; 2013) calls these ‘representational’ and ‘dynamic’ fidelity. Representational fidelity is concerned with matching a model’s structure to the target’s; dynamic fidelity matches the outputs of model and target systems. In different contexts we care more or less about each desiderata. As a first pass, it seems as if when we care about dynamic fidelity—matching a model’s output to the world—we are not required to take models as representations in Walton’s sense. After all, in such circumstances we only care that the model provides the appropriate output.

In the third stage of pump selection, a pump is picked from amongst the standard options by, effectively, matching the curve generated by the pipe equation to the curve relating to the pressure output of each particular pump. This process is carried out automatically: a piece of computer software matches pump to well. This ensures that a pump is selected which is able to overcome the pressure, flow and friction from the required volumes of water. There is a broad sense in which the pump-curves ‘represent’ features of the pipe. But they do not do so as fictionalists require. That is, their functioning does not turn on their being props which demand certain imaginings in games of make-believe. It is hard to see how this could be so, given that the matching process is carried out by a computer. Moreover, even if the task was carried out by a human, they wouldn’t have to know what they were actually doing—selecting the optimal pump given the requirements of the case—to successfully achieve the task. All they would need to do is match the curves as best they could. Such models could be used as props, but this makes no in-principle difference to their capacity to perform the task. In short, the model’s success doesn’t require that it licenses games of make-believe.

One may object that in designing the models we must take them as representational in Walton’s sense. That is, designing a model requires that we partake in the relevant game of make-believe (via more or less explicitly specifying a set of rules of generation and constructing some prop). Even if this is right, I don’t see how the point carries over to the model’s function once it is constructed. It might be a necessary condition that, were the model to be taken as a representation in those terms, it would generate the relevant truths. But this is a weak condition: presumably any object could operate as any number of props in any number of games. Further, one might argue that non-fictional models are not models. This strikes me as unmotivated—my father utilizes a range of proxies to aid his selecting of a real-world pump. These proxies play a variety of roles, some fictional and others not, but all are surely part of the activity of modeling. I imagine that many might be attracted to this last point, since such cases are not viewed as problem cases, but are simply excluded from accounts of modelling. However, such exclusions seem ad hoc. If modeling accounts are supposed to be exhaustive, then we should prefer an account which happily accommodates them.

We can take the case study which opened the paper, then, as involving three kinds of models, delineated in terms of their function. First, preliminary models. In pump selection, models are constructed in stages, preliminary models acting as scaffolds for more detailed, more targeted models. Preliminary models are often used to aid in the imagining of the final product, but are not properly understood in fictionalist terms because their success does not turn on their saying (approximately) true things, or being (approximately) accurate representations, or possessing any other sufficiently detailed resemblance relation with a target system. Their role is to provide a basis to build further models in a dynamic interaction with the target system, and thus they play a crucial role in how the designed object turns out. This is world-directed—the purpose of the model is to build something, after all—but its success in that world-directed function does not turn on its partial truth, or on property comparisons. Preliminary models make trouble for any account which cashes out model-world relations in terms of resemblance (thus including many structuralist accounts).

Second, fictional models. These, like the model which my father uses to determine the required properties of the future pump, do function as the fictionalist would have it. Which is to say, the models act as props which urge games of make-believe by which the model says true things of the future pump.

Third, procedural models—we see these in the final stage, where the optimal pump design is selected. In this context, the model fulfilling its function doesn’t require that it be representational. Here, we simply care about its output: by matching the well system curves to pump pressure curves, the right selection is identified. To do so, we do not need to take the well system curves or the pump pressure curves as representing wells or pumps in Walton’s sense. We simply need to know that following this procedure will provide the result we need.

The lesson is that—particularly in engineering—there are world-directed uses of models which fictionalists cannot account for.[9]

6. Models as Tools

In this section I co-opt work from the philosophy of artifacts to argue that we should understand models as tools.

The content of a story is determined by the rules of generation and the props. The author controls these via how they design the props (say, the words they write). A model’s content, by contrast, depends upon what use it is put to. Sometimes, my father might use the mass-flow equation in an explanatory context, for instance, in accounting for how some pump has malfunctioned. Here, a fictionalist treatment is attractive: the success of the model (that it facilitates a good explanation) turns on it having the right resemblance relation to the pump in question. In other contexts, the mass-flow equation is a preliminary model. As we saw in the last section, under such circumstances the model has a different model-world relationship insofar as its success does not turn on it resembling the target system (at least, on the fictionalist understandings of ‘resemblance’ and ‘target’ I have discussed). It seems reasonable to say that, when it is put to different uses, the content of the mass-flow equation changes. Content being relative to use is, as we shall see, a central component of artifacts. It is my claim that understanding models qua tools is deeper, more unified and more metaphysically kosher than understanding models qua fictions. I’ll start by explaining what tools are. I will then attempt to answer the semantic and model-world questions by equating models with tools. In the next section, I’ll turn to the metaphysical question.

Some philosophers (particularly Amie Thomasson 1999) have argued that some apparently problematic objects such as fictional characters are abstract artifacts. By ‘abstract’, they mean lacking spatio-temporal location, rather than possessing only structural properties. On such views, fictional characters are something like platonic objects which bear concrete properties, but differ insofar as they are created. I want to distinguish the view I am exploring here from such cases, and so will stipulate a class of artifacts: ‘tools’.[10]

Tools are a kind of artifact, specifically material objects which are used to manipulate other material objects.[11] Sewing needles, for instance, allow us to convert pelts and other materials to tailored clothing. Tools are often designed, but are not necessarily so. Both a hammer and a rock can be used as a hammer. The suitability of a tool depends upon its material properties and the task at hand. The size of a needle’s eye, for instance, is more or less appropriate depending on the diameter of thread used. Two kinds of content attach to tools, then. There are truth-apt propositions about a tool’s material features: the weight and size of a needle, the radius of its eye, and so forth. But there are also (what I will call) success conditions. Some features of a tool are relevant to meeting success conditions and others are not. A set of tools frequently discussed by philosophers of science are instruments such as telescopes, spectrometers, and so forth. The philosophy of artifacts has some helpful conceptual machinery, which I’ll co-opt.

Although paradigm artifacts—sewing needles, hammers—are material objects, they are also intentional. They are creations, ontologically dependent on their creators (Hilpinen 1992; Thomasson 2007). However, the creator of an artifact need not actually change the artifact’s material properties—one simply has to put it to the relevant use. By using a stone to hammer in tent pegs, I use the stone as a hammer. As such, I can understand the properties of tools in terms of some function F: some properties are relevant for the object’s suitability for F and others are not. I’ll call these relevant properties F-properties. The size of a sewing-needle’s eye is an F-property, as different sizes are more or less appropriate for being threaded by different materials. A sewing needle’s colour is irrelevant for this purpose, and so is not an F-property in this context.

We can evaluate the success of an artifact on the basis of three criteria (paraphrased from Hillipinen 2011). First, the degree of fit between the intended object and the object’s actual character. That is, did the creator make what they intended to? Second, the degree of fit between the intended object’s F-properties and its function. That is, whether the object the creator intended to make would be suitable for their purpose. Third, the degree of fit between the actual object’s F-properties and F. Roughly, does the actual object do what we want it to? We can, then, distinguish between two classes of claims about tools: claims about material properties, and F-claims—claims which link the properties of an artifact to its purpose via the three criteria.

So, tools are a kind of artifact: they are built, intentional (that is, functional) objects. Tools have two kinds of properties: material features and functional features, F-properties. Material features are simply the properties of the tool qua material object. Tools have a weight, a constitution, they behave in certain ways, and so forth. F-properties are the physical features combined with a ‘suitability for’ condition—F-claims—where suitability is indexed to whatever it is the tool is being used for.

Recall the distinction between a model’s vehicle and content. The vehicle is the medium through which the content is expressed. To take models as tools, we identify a standard tool’s ‘material features’ with the features of the vehicle, and F-properties with the model’s content. The F-properties are the subset of the vehicle-properties which can be appropriately coupled with ‘suitability-for’ claims. For instance, my father’s hydraulic line diagrams may be sketched using various colours—colour, then, is a vehicle-property—however, it is not typically an F-property as colour does not facilitate the diagram’s fulfilling its purpose. Its 2-dimensionalism is often an F-property, as the added simplicity allows better understanding of the relevant features of pump design. This move allows us to answer the semantic question and the model-world question, as follows.

The semantic question asks us to understand claims about models. When my father says “the pressure is proportional to the square of the flow”, we want this claim to come out as true, even though it is strictly speaking false when taken as a claim about pressure and flow in the world. On the tool view, this should be read in reference to the model’s vehicle. That is, the truth conditions for the claim turn on the properties of the vehicle and where relevant to how we construe those properties. These are not restricted to F-properties. My father’s statement about pressure and flow picks out the relationship between two variables identified as ‘pressure’ and ‘flow’ in the model. It is true, just in case the stated relationship between the variables is instantiated in the relevant vehicle. That is, do the correct physical manipulations of the tool (carrying out calculations on paper, running a computer simulation, etc.) result in the relevant behavior? If so, the claim is confirmed.

The model-world question asks us how it is that models tell us about the world. On the tool view, models tell us about the world in virtue of being adequate for some purpose. That is, their F-properties promote the kind of model output which is desired. These are enormously varied. In many contexts—those which fictionalists focus on—the function of the model is to serve as a representation in Walton’s sense. In explaining why a pipe has certain properties, my father might refer to the model claim that “the pressure is proportional to the square of the flow”. In this context, the model’s aim is usefully understood as acting as a prop in a game of make-believe, or as a modified, exaggerated description of the actual well system. However, in other contexts the model might act as a calculating device, or a way of cleaning data, or as a repurposable object, or so on. In these contexts, the model’s success turns on the criteria discussed above.

For instance, consider preliminary models. In our case study, these include the simple mass-flow equation, and the more complex model used to determine Ptmax (the maximal required pressure to get water into the tank). In the last section, I argued that taking these as generating (partially) true statements about the world, or licencing property comparisons, doesn’t capture how they tell us about the world. They are world-directed in virtue of being the basis of—a scaffold for—further models. On the tool view, we can understand preliminary models in terms of their function, that is, the relationship between F and the model’s F-properties. For preliminary models in engineering, F is the facilitation of the construction of further models which will determine the ultimate properties of what is being designed or selected. The F-properties in question, then, are those features of the model in virtue of which it is a good scaffold. The model determining Ptmax takes into account some of the features which will eventually matter for the pump’s construction, such as draw-down amount and the distance from the (assumed) pump discharge point to the floor, however it misses other necessary components such as seasonal well characteristics, atmospheric pressure, etc. The point of determining Ptmax in isolation of these other factors is in part to simplify the selection process, and to narrow the search space. The model is a good one insofar as its F-properties (that it takes into account draw-down, but ignores atmospheric pressure, say) facilitate those functions. It doesn’t succeed in virtue of representing the pump which is ultimately selected, but by aiding in the construction of models which do, and by enabling an appropriate dynamic relationship with the design and construction processes themselves.

Notice that, on this view, we can happily accommodate fictionalism (and recall that my objection to fictionalism turns on the idea that fictionalism is supposed to be a complete account of modeling!). There are some uses to which we put objects that involve taking them to have representational content. Under such circumstances—when we use a model to explain the behavior of a target system, for instance—the F-properties that matter are those which make for a good representation. In short, what makes for a good prop. Moreover, this is amenable to both direct and indirect views. On an indirect view, we take the model descriptions as props, while on the direct view the target itself plays this role. In either case, they can be conceived of as material objects repurposed as representational tools. The basic features of Walton’s account are available. However, tools need not be representational, and so neither do models.

It is time to turn to the metaphysical question.

7. Models as Material Objects

Something may have struck you as odd in the last section: I defined ‘tools’ as material objects, not merely concrete objects, the bearers of non-structural properties, but as material objects. I want to explore taking this quite literally. As we have seen, Levy’s deflationary move is to identify the model system with the target system: literally speaking, there is no model system, but rather a description of the target, which emphasizes some aspects over others. In Section 4 I argued that this view was problematic for preliminary models: their success does not turn on describing targets, but rather on scaffolding further model construction. The position I want to explore is similarly deflationary, but avoids this kind of objection. I suggest that in some circumstances we should equate the model system with the model’s vehicle (or description). It is an open question whether vehicles are necessarily material, but it’s worth examining a view which takes them to be. Which is to say, could models be, properly speaking, just the inscription of the equation, or the mental operations and imaginings, or the instantiated software, etc.?[12]

Many philosophers have emphasized the materiality of models, often while providing accounts similarly pragmatic to mine (Boumans 2012; Knuuttila 2011; Parker 2009a; 2011). I don’t think incorporating materiality is necessary for capturing modeling practice—fictionalist appeals to ‘props’, it strikes me, happily accommodate this—however, taking them as material objects is amenable to a deflationary metaphysics about models.

Consider the mass-flow equation. This is realized by many model descriptions: a scribbled inscription, in prose, as an equation, instantiated by computer software, mentally represented, and so forth. By the tool-view, we equate models with vehicles. In each realization, we can understand the model in terms of that material object’s (the model description’s) behavior. In a computer, various physical components, microchips, processors, etc., undergo particular processes and produce particular behaviors depending on how we program and manipulate them. Pen-and-paper models are perhaps best understood as being coupled with cognitive processing. In solving an equation by hand, the inscriptions and my brain activity interact such that regular behaviors emerge. In each case, it seems coherent to understand the model—the tool in question—as a vehicle, and the vehicle as being a material object.

By this view there is not, metaphysically speaking, a ‘model’ independent of the model description and target system. There is a vehicle, and there are the functions to which vehicles are put. We equate the model with its vehicle, and take that object as a tool with F-properties relating to the target.

Is equating models with vehicles sufficient to make them material? Not necessarily. I’ve described tools as material objects: instantiated, complex, and boasting spatio-temporal location. This is uncontroversial concerning hammers and sewing needles, and presumably also for physical models—but surely this is an odd thing to say about mathematical models. Here, it might be tempting to draw the notion of a model’s vehicle apart from its physical realization, to say that an equation can be represented in many different mediums, but its representational content—the object which bears that content—is mathematical rather than material or concrete. Deciding whether material or mathematical objects ‘bear’ mathematical content depends on answers to questions about the nature of mathematical truth, questions which are above my paygrade in this context. Suffice to say, nominalist or anti-realist answers to that question would allow us to identify vehicles with model descriptions, as would views which take mathematical truth to be ‘contained’ in material objects. Even if we admit abstract vehicles in some mathematical contexts, the tool view still has the advantage of accommodating preliminary and procedural models. There are two related objections I want to cover.

First, the ‘models-as-vehicles’ view is counterintuitive. Imagine my father scribbles otherwise identical equations on two separate pieces of paper. Surely these are instances of the same model, as opposed to two different models as my account demands. There appear to be differences in how we intuitively treat objects like sewing needles and models—we are keener to distinguish between needle-tokens than we are between model-tokens.

Second, some philosophers take it that a criterion for a successful account of models and modeling is successfully accommodating the individuation of models (see Frigg 2010; Weisberg 2013). That is, tell us when two models count as the same model, and when they are different models. On the face of it, this makes trouble for my account: if models are vehicles, then it doesn’t seem as if there is a way of unifying them. If I write an equation using paper, or enter it into a computer, surely these are examples of the same model. But on my view this can’t be right, as both models have different material constitution: one is made of paper and graphite, the other of silica. Moreover, the individuation of models helps facilitate communication about, and the study of, models—it helps solve epistemic issues.

These objections are too quick, however. Tools are a classic classifiable object. Sewing needles are categorized based on their different points: ball-point needles are ideal for knit fabrics due to their not separating fibres, while regular-point needles are used for woven fabrics. Restricting ourselves to needles for hand-sewing, various types of needle with various lengths, bendability, sharpness, and eye-size are distinguished. These include long, thick, darning needles with large eyes, long, thin, beading needles, and curved upholstery needles. There is nothing at all mysterious about these classifications: needle-kinds are classified in terms of physical properties and intended purposes. And just the same may be said for models. That is, there are many very similar tokens of model types, such as inscriptive and software versions of the mass-flow equation. However, this range of apparently very disparate vehicles share relevant F-properties, and so are both suitable for various uses and categorizable on that basis. They are tokens of the same model type in virtue of having relevantly similar F-properties. This enables the kind of individuation which is required for the epistemology of modeling. It is not in virtue of any old vehicle-properties that two models are of the same type, but in virtue of those vehicle properties which are properly coupled to the model’s use; its F-properties.

Regardless, I am not moved to see the individuation of models as a metaphysically deep issue. Like paradigm tools, models are used in such a variety of ways, and are often so easily repurposed, that answering when two models are ‘the same’ looks like a pragmatic, as opposed to metaphysical, question.

8. Conclusion

Philosophers concerned with modeling often stress the importance of capturing their use in practice—and indeed modellers do often interact with, discuss, and conceive of their models in fictionalist ways. And so an account of modeling must be sensitive to this. However, I have argued that fictionalism is incomplete: as an overall account of scientific modeling the view is insufficient. It is insufficient because some model purposes are not fictional, which is to say do not involve acting as props in games of make-believe. Instead, we should identify models with their vehicles, (potentially) material objects which are suitable for particular tasks. That is, models are tools. The crucial advantage of the tool-based account, in my view, is its capacity to flexibly account for both fictional and non-fictional models. As such, it provides a better overall picture of the practice.

Acknowledgements

I am grateful to Mike Currie, Arnon Levy and Kirsten Walsh for valuable and insightful comments on earlier drafts, as well as two anonymous referees for Ergo. Also thanks to Megan Delehanty and Adam Toon for fruitful discussion regarding the paper. I presented an early draft at the IRH in Bucharest and received very useful feedback. This publication was made possible through the support of a grant from Templeton World Charity Foundation. The opinions expressed in this publication are those of the author and do not necessarily reflect the views of Templeton World Charity Foundation.

References

• Boumans, Marcel (2012). Mathematics as Quasi-Matter to Build Models as Instruments. In Dennis Dieks, Weceslao J. Gonzalez, Stephan Hartmann, Michael Stöltzner, and Marcel Weber (Eds.), Probabilities, Laws, and Structures (307–318). Springer. https://doi.org/10.1007/978-94-007-3030-4_22
• Cartwright, Nancy (1983). How the Laws of Physics Lie. Clarendon Press. https://doi.org/10.1093/0198247044.001.0001
• Feibleman, James K. (1967). The Philosophy of Tools. Social Forces, 45(3), 329–337. https://doi.org/10.1093/sf/45.3.329
• Frigg, Roman (2010). Models and Fiction. Synthese, 172(2), 251–268. https://doi.org/10.1007/s11229-009-9505-0
• Frigg, Roman and James Nguyen (2016). The Fiction View of Models Reloaded. The Monist, 99(3), 225–242. https://doi.org/10.1093/monist/onw002
• Giere, Ron (1988). Explaining Science: A Cognitive Approach. University of Chicago Press. https://doi.org/10.7208/chicago/9780226292038.001.0001
• Godfrey-Smith, Peter (2006). The Strategy of Model-Based Science. Biology and Philosophy, 21(5), 725–740. https://doi.org/10.1007/s10539-006-9054-6
• Godfrey-Smith, Peter (2009). Models and Fictions in Science. Philosophical Studies, 143(1), 101–116. https://doi.org/10.1007/s11098-008-9313-2
• Hilpinen, Risto (1992). On Artifacts and Works of Art. Theoria, 58(1), 58–82. https://doi.org/10.1111/j.1755-2567.1992.tb01155.x
• Hilpinen, Risto (2011). Artifact. In Edward N. Zalta (Ed.), The Stanford Encyclopedia of Philosophy (Winter 2011 Edition). Retrieved from http://plato.stanford.edu/archives/win2011/entries/artifact/
• Knuuttila, Tarja (2011). Modelling and Representing: An Artefactual Approach to Model-Based Representation. Studies in History and Philosophy of Science Part A, 42(2), 262–271. https://doi.org/10.1016/j.shpsa.2010.11.034
• Levy, Arnon (2012). Models, Fictions, and Realism: Two Packages. Philosophy of Science, 79(5), 738–748. https://doi.org/10.1086/667992
• Levy, Arnon (2015). Modeling without Models. Philosophical Studies, 172(3), 781–798. https://doi.org/10.1007/s11098-014-0333-9
• Lewis, David (1986). On the Plurality of Worlds. Blackwell.
• Parker, Wendy S. (2009a). II—Confirmation and Adequacy-for-Purpose in Climate Modelling. Aristotelian Society Supplementary Volume, 83, 233–249. https://doi.org/10.1111/j.1467-8349.2009.00180.x
• Parker, Wendy S. (2009b). Does Matter Really Matter? Computer Simulations, Experiments, and Materiality. Synthese, 169(3), 483–496. https://doi.org/10.1007/s11229-008-9434-3
• Parker, Wendy S. (2011). Scientific Models and Adequacy-for-Purpose. Modern Schoolman: A Quarterly Journal of Philosophy (Proceedings of the 2010 Henle Conference on Experimental & Theoretical Knowledge), 87(3–4), 285–293.
• Salis, Fiora (2016). The Nature of Model-World Comparisons. The Monist, 99(3), 243–259. https://doi.org/10.1093/monist/onw003
• Strevens, Michael (2008). Depth: An Account of Scientific explanation. Harvard University Press.
• Suarez, Mauricio (2003). Scientific Representation: Against Similarity and Isomorphism, International Studies in the Philosophy of Science, 17(3), 225–244. https://doi.org/10.1080/0269859032000169442
• Thomasson, Amie L. (1999). Fiction and metaphysics. Cambridge University Press.
• Thomasson, Amie L. (2007). Artifacts and Human Concepts. In Eric Margolis and Stephen Laurence (Eds.), Creations of the Mind: Theories of Artifacts and Their Representation (52–73). Oxford University Press.
• Thomson-Jones, Martin (2010). Missing Systems and the Face Value Practice. Synthese, 172(2), 283–299. https://doi.org/10.1007/s11229-009-9507-y
• Toon, Adam (2010). The Ontology of Theoretical Modelling: Models as Make-Believe. Synthese, 172(2), 301–315. https://doi.org/10.1007/s11229-009-9508-x
• Toon, Adam (2011). Playing with Molecules. Studies in History and Philosophy of Science Part A, 42(4), 580–589. https://doi.org/10.1016/j.shpsa.2011.08.002
• Toon, Adam (2012). Models as Make-Believe. Palgrave-Macmillan. https://doi.org/10.1057/9781137292230
• Walton, Kendall L. (1990). Mimesis as Make-Believe: On the Foundations of the Representational Arts. Harvard University Press.
• Weisberg, Michael (2007). Who is a Modeler? The British Journal for the Philosophy of Science, 58(2), 207–233. https://doi.org/10.1093/bjps/axm011
• Weisberg, Michael (2013). Simulation and Similarity: Using Models to Understand the World. Oxford University Press. https://doi.org/10.1093/acprof:oso/9780199933662.001.0001
• Yablo, Stephen (2014). Aboutness. Princeton University Press.

Notes

1. See, e.g., Cartwright (1983), Frigg (2010), Godfrey-Smith (2009), Toon (2010; 2012), Levy (2012; 2015).

2. The term ‘abstract’ is notoriously difficult (Lewis 1986) except where noted I will take an abstract entity to be one which only possesses structural properties (Levy 2015; Thomson-Jones 2010).

3. See Weisberg (2013) for a response to these species of worry.

4. This is due to Weisberg’s reliance on modellers construing the structural properties of models ‘as if’ they are instantiated: “Fictions are crucial to [Weisberg’s] understanding of the model world relation to the extent that model construals involve apparent reference to hypothetical systems having features (attributes and mechanisms) that only concrete objects can have” (2016: 257).

5. Walton himself is not so motivated by metaphysical deflation, but fictionalists about models certainly are.

6. As Salis has put it, “There is no rabbit population instantiating the properties that are compared to those of a real rabbit population. So, on this interpretation, model-world comparisons are still false” (2016: 257).

7. Levy (2012; 2015) and Toon (2012) explicitly, although Strevens (2008: Chapter 7) could potentially be read in these terms.

8. Salis (2016) provides a fictionalist account of the model-world relationship, but she doesn’t discuss, and it isn’t clear to me, whether it can manage the problem cases in Section 5.

9. A referee makes the fascinating suggestion that instead of considering these as different models, we instead take them as different stages in the life of a single model. I think taking models in such a dynamic way fits nicely with the account I provide in the next section, but it is not obvious to me how such a move might provide a way out of the two problem cases I present for fictionalists.

10. I’m not sure whether we should take ‘fictions’, generally speaking, to be tools, as there may be contexts where the content of a fiction is not sensitive to its use. However, it is part of my view that the sense of fictions relevant to scientific modelling can be captured by the notion of ‘tool’ I develop. Further, different notions of fiction might be more or less conducive to being captured in tool-like terms. Walton’s view is particularly amenable—props are reasonably considered tools to aid imagination. So far as I can tell, my view doesn’t turn on these issues.

11. My use of the term ‘tool’ is stipulative, although identifying tools with material objects follows Fiebleman (1967).

12. I take Wendy Parker’s (2009b) argument that we understand simulation studies as manipulations of actual physical systems—typically the computers on which the studies are run—to be suggestive of this kind of view.