A New Paradigm for Epistemology: From Reliabilism to Abilism

Abstract:

Contemporary philosophers nearly unanimously endorse knowledge reliabilism, the view that knowledge must be reliably produced. Leading reliabilists have suggested that reliabilism draws support from patterns in ordinary judgments and intuitions about knowledge, luck, reliability, and counterfactuals. That is, they have suggested a proto-reliabilist hypothesis about “commonsense” or “folk” epistemology. This paper reports nine experimental studies (N = 1262) that test the proto-reliabilist hypothesis by testing four of its principal implications. The main findings are that (a) commonsense fully embraces the possibility of unreliable knowledge, (b) knowledge judgments are surprisingly insensitive to information about reliability, (c) “anti-luck” intuitions about knowledge have nothing to do with reliability specifically, and (d) reliabilists have mischaracterized the intuitive counterfactual properties of knowledge and their relation to reliability. When combined with the weakness of existing arguments for reliabilism and the recent emergence of well-supported alternative views that predict the widespread existence of unreliable knowledge, the present findings are the final exhibit in a conclusive case for abandoning reliabilism in epistemology. I introduce an alternative theory of knowledge, abilism, which outperforms reliabilism and well explains all the available evidence.

Keywords: knowledge; knowledge attributions; luck; counterfactuals; ability; abilism; reliabilism

1. Introduction

Contemporary philosophers have hotly debated the relationship between reliability and epistemic justification. Some argue that justification requires reliability (Goldman 1979; Swain 1981; Alston 1988; Greco 2013), while others roundly reject this (e.g., Lehrer & Cohen 1983; Cohen 1984; Foley 1985; Feldman 2013). By contrast, virtually every philosopher to address the matter accepts that knowledge requires reliability (e.g., Russell 1948; Sellars 1963; Dretske 1971; Armstrong 1973; Nozick 1981; Goldman 1986; Sosa 1991; Alston 1993; Plantinga 1993; Heller 1995; Zagzebski 1996; Lehrer 1997; Williamson 2000; Greco 2000; BonJour 2002; Kornblith 2002; Riggs 2002; Cohen 2002; Feldman 2003; Roush 2005; Fumerton 2006; Pritchard 2009; Foley 1985 and Sartwell 1992 dissent). On this popular view, knowledge must be produced by abilities (processes, faculties, powers, etc.) that “will or would yield mostly true beliefs,” where an ability yields mostly true beliefs only if “considerably more than half” of the beliefs it produces are true (Alston 1995: 8–9; see also Vogel 2000; Comesaña 2002: 249; Goldman 2008; for a more extensive list of citations and quotations, see Turri 2015a). Call this consensus view knowledge reliabilism. Adapting a Quinean coinage, it’s not unfair to label knowledge reliabilism the central dogma of contemporary epistemology.

The literature contains surprisingly little explicit argumentation for knowledge reliabilism (hereafter just “reliabilism”). It is often just asserted, without elaboration, that knowledge requires reliability. The main passage cited in favor of reliabilism is a brief explanatory argument from an early paper by Alvin Goldman (1979), later dubbed the “master argument” lending reliabilism “powerful prima facie support” (Goldman 2012: 4). Goldman first notes that knowledge must be appropriately caused and then asks what kind of causes yield knowledge.[1] Goldman produces two lists. One list features processes that intuitively do produce knowledge: perception, introspection, memory, and “good reasoning.” The other list features processes that intuitively do not: “wishful thinking,” “mere hunch,” “guesswork,” and “confused reasoning.” Goldman notes that members of the first list all seem to be reliable, whereas members of the latter all seem to be unreliable. He then proposes an explanation for this: knowledge requires reliability.

But Goldman doesn’t consider alternative explanations. For example, the hypothesis that knowledge requires ability, reliable or not, can explain the membership of these lists. The list of processes that produce knowledge includes cognitive abilities to detect, discover, and retain truths; the list of processes that don’t produce knowledge doesn’t include abilities of detection, discovery, and retention. The weaker abilist hypothesis renders the reliabilist hypothesis otiose.

Not only is the best prima facie evidence for reliabilism equivocal, there are also positive arguments for the possibility of unreliable knowledge (Turri 2015a). One such argument begins with the observation that achievements can be unreliably produced. For example, human toddlers around twelve months old are highly unreliable walkers, but many of their early steps are genuine achievements that manifest their blossoming bipedalism. To take a less cuddly example, hockey players fail to score a goal on approximately ninety percent of their attempts, but many of their goals are genuine achievements that manifest impressive athletic ability. More generally, achievements populate the road to proficiency in many spheres, despite our unreliability. This is true in art, athletics, politics, oratory, music, science, and elsewhere. If achievement in all these spheres tolerates unreliability, then knowledge probably does too. For knowledge is a cognitive achievement, so absent special reason to think otherwise we should expect it to share the profile of achievements generally. But we’ve been given no special reason to suppose that knowledge differs in this regard. At this point, the balance of evidence has tipped against reliabilism, even if popular professional opinion has not.

However, some have suggested a possible alternative source of evidence for reliabilism. The suggestion taps into a deep and wide-ranging tradition in contemporary epistemology, which prizes a theory of knowledge that can explain our ordinary concept of knowledge and knowledge attributions (Austin 1956; Unger 1975; Dretske 1981; Stroud 1984; Vogel 1990; Craig 1990; DeRose 1995; Hawthorne 2004; Stanley 2005; Fantl & McGrath 2009; Turri 2011).

The basic idea is that patterns in ordinary judgments and intuition support reliabilism. For example, John Greco claims that reliabilism is attractive because it “explains a wide range of our intuitions regarding what does and does not count as knowledge,” and we can “gain insight and understanding into what knowledge is” by “reflecting on our thinking and practices” surrounding knowledge (2010: 4–6). Fred Dretske defends an information-theoretic version of reliabilism partly on the grounds that it well fits “ordinary, intuitive judgments” (1981: 92ff; see also 249, Footnote 8). Edward Craig advocates a version of reliabilism on the grounds that it “matches our everyday practice with the concept of knowledge as actually found,” that it is a “close fit to intuitive extension of ‘know’” (1990: 3–4).[2] Ernest Sosa claims that reliabilism is a theoretical “correlate” of “commonsense” epistemology (1991: 100). Goldman argues that one “proper task of epistemology is to elucidate our epistemic folkways,” and that an adequate epistemology must “have its roots in the concepts and practices of the folk” (1993: 271). Goldman further argues that “folk” epistemology is an incipient form of reliabilism: “our inclinations” and “intuitions” about knowledge are keyed to reliability.

Call this the proto-reliabilist hypothesis about folk epistemology. This paper seeks evidence for the intriguing proto-reliabilist hypothesis. Taking a cue from Goldman, I treat the investigation as “a scientific task” and adopt the method of controlled experimentation typical in cognitive science (Goldman 1993: 272; see also Goldman & Olsson 2009: 35, who advocate explaining “commonsense epistemic valuations in a scientific fashion, especially by appeal to psychology”).

The proto-reliabilist hypothesis generates testable implications. There are at least four principal implications, either straightforwardly entailed by the hypothesis or suggested by reliabilists themselves. First and foremost, people should not count unreliably produced belief as knowledge. For example, if an ability produces only ten percent or thirty percent true beliefs, then the beliefs it produces should not be judged knowledge. Second, and closely related, vast and explicit differences in reliability should produce large differences in knowledge judgments. Third, reliabilists have claimed that their view captures the “fundamental intuition” that knowledge cannot be lucky (e.g., Goldman & Olsson 2009: 38; Heller 1999: 115; see also Heller 1995). Reliability is said to be at the heart of this “anti-luck intuition” (Becker 2006; Greco 2010: Chapter 9; see also Pritchard 2012). So people should count an unreliably produced true belief as lucky and, therefore, not knowledge. Fourth, reliabilists, along with many others, have claimed that knowledge has certain counterfactual properties that are explained or captured by (very high) reliability (Goldman 2008; see also Dretske 1971; Nozick 1981; DeRose 1995; Sosa 1999; Vogel 2000). Reliability is said to be at the heart of these “counterfactual intuitions,” as we might call them. So people should attribute knowledge only if they attribute the counterfactual properties, and they should not count an unreliably produced true belief as having relevant counterfactual properties.

One prior study examined intuitions about a purported counterexample to reliabilism, Keith Lehrer’s Truetemp case (Lehrer 1990: 163–4; Swain, Alexander & Weinberg 2008). But those intuitions pertain to whether reliably produced true belief is sufficient for knowledge, whereas I’ll be concerned with whether it’s necessary. Aside from that one study, prior empirical work has not directly addressed the status of reliabilism in folk epistemology (for overviews, see Alexander 2012; Beebe 2012; Pinillos 2011; Beebe 2014).

The basic approach adopted here is to elicit judgments about simple cases that vary how reliably beliefs are formed. The main finding is that the proto-reliabilist hypothesis is clearly false. Commonsense fully embraces the possibility of unreliable knowledge: rates of unreliable knowledge attribution sometimes reach 80–90%. Knowledge judgments are surprisingly insensitive to information about reliability: people attribute knowledge at similar rates whether the agent gets it right ninety percent of the time or ten percent of the time. Commonsense does share the intuition that knowledge isn’t lucky, but the intuition is keyed to ability, reliable or unreliable, not reliability. Finally, reliabilists have badly mischaracterized the intuitive links among reliability, knowledge and various counterfactual judgments. I propose an alternative hypothesis, abilism, that better explains the findings and integrates them into a broader framework that also explains other surprising recent discoveries.

2. Experiment 1

2.2. Results

Assignment to condition affected response to the knowledge statement.[6] But this was because mean response in the False condition was significantly lower than in Ten and Ninety.[7] Mean response in Ten and Ninety didn’t differ significantly.[8] The mode was “strongly disagree” (= 1) in False, “agree” (= 5) in Ten, and “strongly agree” (= 6) in Ninety.

Figure 1. Mean agreement with the knowledge statement on a 1 (strongly disagree) – 6 (strongly agree) scale. Error bars represent bootstrapped 95% confidence intervals.

3. Experiment 2

3.2. Results

If the proto-reliabilist hypothesis is true and the concerns raised about the earlier results are legitimate, then we should observe two things. First, people should attribute knowledge significantly more in the True Ninety condition than in the True Ten condition. Second, people should attribute knowledge at rates below chance in the True Ten condition. Aside from either of those predictions, we should expect people in each False condition to attribute knowledge at rates below chance.

None of the predictions turned out true.[11] First, in the True Ninety condition, 87% of participants attributed knowledge, which was not significantly more than the 75% who attributed knowledge in the True Ten condition.[12] Second, participants in the True Ten condition attributed knowledge at rates significantly above chance.[13] Third, only 13% of participants in the False Ten condition attributed knowledge, which is far below chance,[14] but a surprisingly high 39% attributed knowledge in the False Ninety condition, which does not differ significantly from chance.[15] (Note: this puzzling finding in False Ninety does not replicate in Experiment 3, so it might be an anomaly.)[16] Knowledge attribution in False Ninety was significantly higher than in False Ten.[17]

Figure 2. Experiment 2: Percentage of participants attributing knowledge.

Question 2 serves as a manipulation check. Response to this question cannot be interpreted very well in the False conditions because participants were given no positive information about Alvin’s reliability, only negative information about what the relevant percentage is not. But this is not worrisome because it is beside the point of including the manipulation check. The check was included to measure how participants in True conditions assess Alvin’s reliability. More specifically, it was included to answer two questions. First, do participants rate Alvin’s reliability significantly higher in True Ninety than in True Ten? Second, do participants in True Ten attribute knowledge despite rating Alvin as unreliable?

The answer to both questions is “yes.” On the one hand, participants rated Alvin’s reliability significantly higher in True Ninety than in True Ten.[18] Mean reliability rating was significantly below the theoretical midpoint (= 3.5) in True Ten, and it was significantly above the midpoint in True Ninety.[19] On the other hand, among the twenty-one people in True Ten who attributed knowledge, mean reliability rating was significantly below the midpoint.[20] The modal response in this group was “strongly disagree” (= 1). Moreover, mean reliability rating in this group did not differ significantly from the mean for those in True Ten who denied knowledge.[21]

4. Experiment 3

4.2. Results

If the concern raised about Experiment 2 was well founded, then the results this time will be more favorable to the proto-reliabilist hypothesis. By contrast, if the results are broadly similar to those observed in Experiment 2, then the earlier concern was not well founded.

The results replicated the findings from Experiment 2.[23] In the True Ninety condition, 74% of participants attributed knowledge, which was exactly the same as in the True Ten condition.[24] Participants in the True Ten condition attributed knowledge at rates significantly above chance.[25] Only 17% of participants in the False Ten condition attributed knowledge, which is far below chance[26] and not significantly different from the 23% who attributed knowledge in the False Ninety condition.[27] (Note: this fails to replicate the puzzling finding in False Ninety in Experiment 2.) Participants rated Alvin’s reliability significantly higher in True Ninety than in True Ten.[28] Mean reliability rating was trending below the theoretical midpoint (= 3.5) in True Ten, and it was significantly above the midpoint in True Ninety.[29] On the other hand, among the twenty-three people in True Ten who attributed knowledge, mean reliability rating was significantly below the midpoint.[30] The modal response in this group was “disagree” (= 2). Moreover, mean reliability rating in this group was non-significantly higher than the mean for those in True Ten who denied knowledge.[31]

Figure 3. Experiment 3: Percentage of participants attributing knowledge.

5. Experiment 4

5.2. Results

The results were very similar to Experiments 2–3. First, in the Reliable True condition, 88% of participants attributed knowledge, which was not significantly more than the 86% who attributed knowledge in the Unreliable True condition.[33] Second, participants in the Unreliable True condition attributed knowledge at rates significantly above chance.[34] Third, only 6% of participants in the Unreliable False condition attributed knowledge, which was not significantly different from the 14% who attributed knowledge in the Reliable False condition.[35] In both False conditions, knowledge attribution was far below chance.[36]

Figure 4. Experiment 4: Percentage of participants attributing knowledge.

Question 2 again served as a manipulation check, included to answer two questions. First, do participants rate Alvin’s reliability significantly higher in Reliable conditions than in Unreliable conditions? Second, do participants in the Unreliable True condition attribute knowledge despite rating Alvin as unreliable? The answer to both questions is “yes.” On the one hand, participants rated Alvin’s reliability significantly higher in Reliable conditions than in Unreliable conditions.[37] On the other hand, among the 31 people in Unreliable True who attributed knowledge, mean reliability rating was significantly below the midpoint (= 3.5).[38] The modal response in this group was “disagree” (= 2). Moreover, mean reliability rating in this group did not differ significantly from the mean rating of those in Unreliable True who denied knowledge.[39]

6. Experiment 5

6.2. Results

The results were very similar to Experiment 4. First, in the Reliable True condition, 80% of participants attributed knowledge, which was not significantly more than the 77% who attributed knowledge in the Unreliable True condition.[42] Second, participants in the Unreliable True condition attributed knowledge at rates significantly above chance.[43] Third, only 13% of participants in the Unreliable False condition attributed knowledge, which was not significantly different from the 7% who attributed knowledge in the Reliable False condition.[44] In both False conditions, knowledge attribution was far below chance.[45] Participants rated Alvin’s reliability significantly higher in True Reliable than in True Unreliable.[46] Mean reliability rating was non-significantly below the theoretical midpoint (= 3.5) in True Unreliable, and it was significantly above the midpoint in True Reliable.[47]

Figure 5. Experiment 5: Percentage of participants attributing knowledge.

7. Experiment 6

7.2. Results

The Percent manipulation was extremely effective.[50] To analyze the results for knowledge judgments, I combined people’s response to the dichotomous knowledge probe with their confidence. For each participant, an answer of “knows” was scored +1 and “only thinks” was scored -1. This score was then multiplied by the participant’s reported confidence (1–6) to generate a knowledge score on a scale that ran -6 (maximum knowledge denial) to +6 (maximum knowledge attribution) (following the procedures of Starmans & Friedman 2012).

Thirty percent accuracy is far less than reliabilism requires for knowledge. So if the proto-reliabilist hypothesis is true, then knowledge scores should be low in the Thirty conditions. Moreover, the difference between thirty and ninety percent accuracy is unmistakably large, so if the proto-reliabilist hypothesis is true, then we should observe a large difference between Thirty Ability and Ninety Ability.

Neither prediction was true. Source significantly affected knowledge scores,[51] but Percent did not.[52] Knowledge scores were significantly above the neutral midpoint (= 0) in both Thirty Ability and Ninety Ability, whereas they were significantly below the midpoint in Thirty Guess and Ninety Guess.[53] Knowledge scores did not differ between Thirty Guess and Ninety Guess,[54] or between Thirty Ability and Ninety Ability.[55]

Figure 6. Experiment 6: mean knowledge scores, derived for each participant by multiplying their dichotomous answer (scored +1 for “knows”, -1 for “only thinks”) by their reported confidence (1 = “not at all confident” to 6 = “completely confident”). Scales ran from -6 to +6. Error bars represent bootstrapped 95% confidence intervals.

8. Experiment 7

8.2. Results

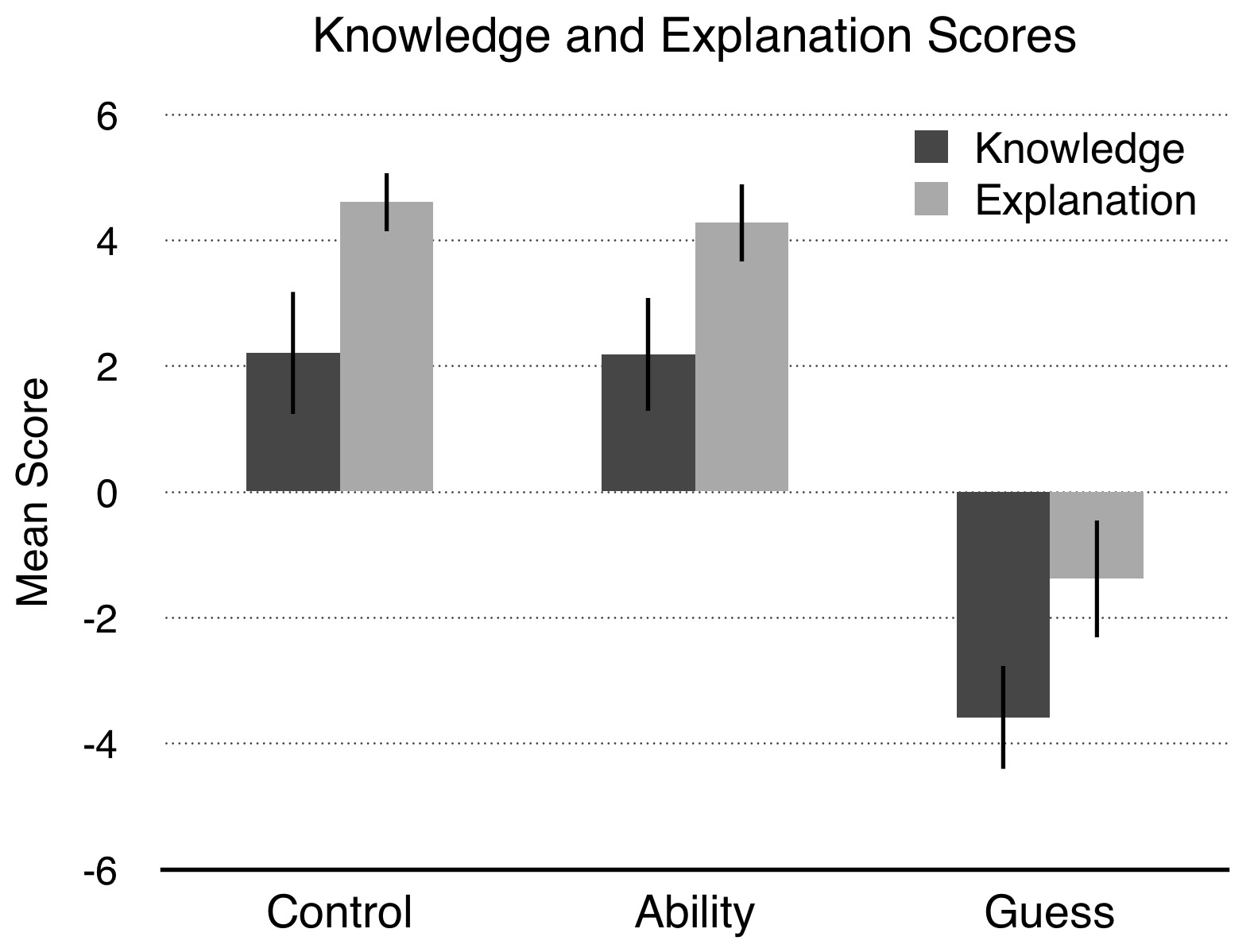
Thirty percent accuracy is far less than reliabilism requires for knowledge. So if the proto-reliabilist hypothesis is true, then knowledge scores should be low in all three conditions. Moreover, if reliabilists are right about the “fundamental” anti-luck intuition, then explanation scores should be low too (i.e., participants should attribute the truth of Carolyn’s belief to luck). By contrast, if abilism better captures the ordinary concept of knowledge and we can gain knowledge through unreliable abilities, then knowledge scores will be high in the Ability condition, and explanation scores should be high too (i.e., participants should attribute the truth of Carolyn’s belief to ability). Moreover, if abilism is true, then merely having the unreliable ability alongside the true belief will not be enough for Carolyn to gain knowledge: the ability also has to produce the true belief. Thus abilism predicts a large difference between knowledge scores in the Ability and Guess conditions.

To analyze the results, I calculated a knowledge score for each participant exactly the same way as in Experiment 6. Analogously, each participant’s response to the explanation probe was scored either +1 (“her ability”) or -1 (“good luck”) and multiplied by the confidence rating, yielding an explanation score on the same -6 to +6 scale. Using these weighted scores allows for more powerful statistical tests and procedures.

Assignment to condition significantly affected knowledge scores.[57] But this was because knowledge scores in Guess were significantly lower than scores in Control and Ability.[58] Knowledge scores in Control and Ability didn’t differ.[59] Knowledge scores were significantly above the neutral midpoint (= 0) in Control and Ability, whereas they were significantly below the midpoint in Guess.[60] Assignment to condition also significantly affected explanation scores.[61] Explanation scores in Control and Ability were significantly above the midpoint, whereas they were significantly below the midpoint in Guess.[62]

Knowledge scores and explanation scores were very strongly positively correlated[63] and, moreover, explanation scores mediated the effect of condition on knowledge scores, suggesting that people attributed knowledge because they attributed Carolyn’s true belief to her unreliable ability.[64] Focusing on just the dichotomous probes, attributing Carolyn’s true belief to ability rather than luck increased the odds of attributing knowledge by over 3800% (or a factor of 38.33).[65]

Figure 7. Experiment 7: Mean knowledge scores and explanation scores (within-subjects). Knowledge scores were derived for each participant by multiplying their dichotomous answer (scored +1 for “knows”, -1 for “only thinks”) by their reported confidence (1 = “not at all confident” to 6 = “completely confident”). Explanation scores were derived for each participant by multiplying their dichotomous answer (scored +1 for “ability”, -1 for “luck”) by their reported confidence. Scales ran from -6 to +6. Error bars represent bootstrapped 95% confidence intervals.

9. Experiment 8

Many philosophers, reliabilists prominently among them, find it intuitive that knowledge has certain important counterfactual properties. Different theorists define these properties differently, the properties go by many different names, and it is widely acknowledged that precisely formulating the properties is a delicate and tricky business (see, for example, Dretske 1971; Goldman 1979; Nozick 1981; DeRose 1995; Sosa 1999; Vogel 2000). But the general outlines of the counterfactual properties are clear enough to begin testing. The basic idea is that knowledge is, or essentially involves, “some variation of belief with the truth” (Nozick 1981: 209). The variation comes in two basic forms, which can be indicated by asking two simple questions. On the one hand, if things had been slightly different, would you still have believed the truth? On the other hand, if things had been slightly different, might you have believed falsely? For present purposes, I will call these properties adherence to truth and resistance to falsehood, respectively.[66]

Some claim that knowledge requires both adherence and resistance, whereas others claim that only one is required; I will ignore this dispute and instead investigate whether commonsense epistemology is implicitly committed to either principle and, if so, its potential connection to reliability. Some claim that knowledge requires even stronger or more elaborate forms of adherence or resistance; I will ignore these proposals and focus only on the basic forms. In order to test for a commitment to adherence, I will ask people whether an agent would still correctly identify the facts in slightly different circumstances. In order to test for a commitment to resistance, I will ask people whether an agent might misidentify the facts in slightly different circumstances. Experiment 8 tests adherence. Experiment 9 tests resistance.

9.2. Results

The proto-reliabilist hypothesis predicts, at the very least, that people will attribute knowledge only if they also attribute adherence. The proto-reliabilist hypothesis also predicts that people will attribute adherence only for reliably produced belief. If the more ambitious claims of some reliabilists are true, then when focusing on cases of true belief, we should also observe a strong positive correlation between knowledge judgments and adherence judgments, and perhaps we will even find evidence that adherence judgments cause or explain knowledge judgment.

To analyze the results, for each participant I calculated a knowledge score in the same way described in earlier experiments. I also calculated an adherence score similarly (“would” scored as +1, “would not” scored as -1, multiplied by reported confidence, 1–6). Higher adherence scores indicate greater adherence to the truth.

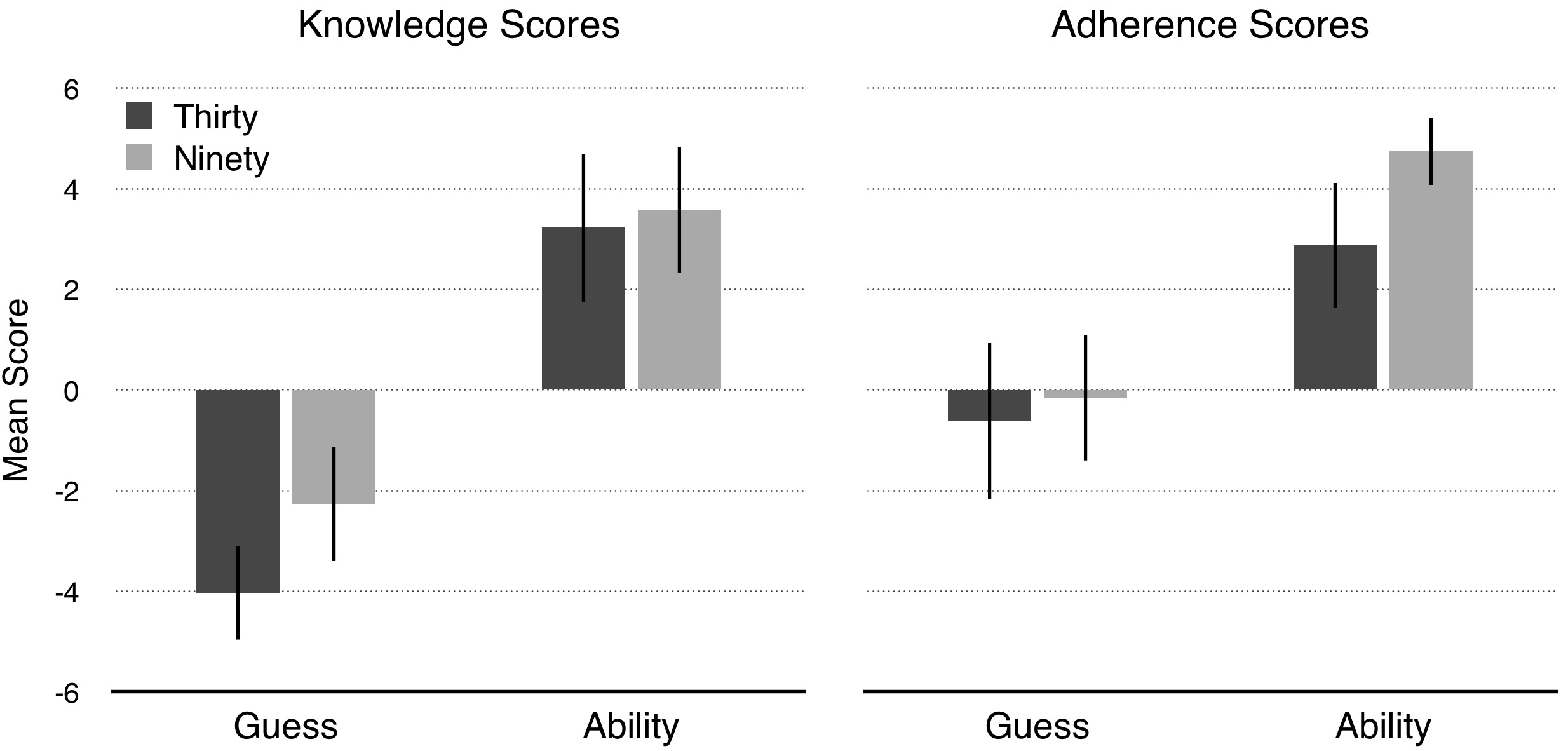
Assignment to condition significantly affected knowledge scores.[68] There was a trending main effect of Percent,[69] a large main effect of Source,[70] and no interaction.[71] Knowledge scores did not differ between Thirty Ability and Ninety Ability,[72] and they were significantly above the neutral midpoint (= 0) in each of those two conditions.[73] Knowledge scores were significantly higher in Ninety Guess than Thirty Guess,[74] but they were significantly below the midpoint in each of those two conditions.[75] Knowledge scores were significantly higher in Thirty Ability than Thirty Guess,[76] and they were higher in Ninety Ability than Ninety Guess.[77]

Assignment to condition significantly affected adherence scores.[78] There was a main effect of Source,[79] a trending main effect of Percent,[80] and no interaction.[81] Adherence scores were significantly higher in Ninety Ability than Thirty Ability,[82] and they were significantly above the neutral midpoint in each of those two conditions.[83] Adherence scores were no different in Ninety Guess and Thirty Guess,[84] and they didn’t differ from the midpoint in either condition.[85] Adherence scores were higher in Thirty Ability than Thirty Guess,[86] and they were higher in Ninety Ability than Ninety Guess.[87]

Overall, knowledge scores and adherence scores were moderately positively correlated.[88] However, unlike in Experiment 7 where explanation scores mediated the effect of condition on knowledge scores, in the present experiment adherence scores did not mediate the effect of condition on knowledge scores.[89],[90]

Figure 8. Experiment 8: Left panel: mean knowledge scores, derived for each participant by multiplying their dichotomous answer (scored +1 for “knows”, -1 for “only thinks”) by their reported confidence (1 = “not at all confident” to 6 = “completely confident”). Right panel: mean adherence scores, derived for each participant by multiplying their dichotomous answer (scored +1 for “would”, -1 for “would not”) by their reported confidence. Scales ran from -6 to +6. Error bars represent 95% confidence intervals.

10. Experiment 9

10.2. Results

Preliminary analysis revealed that people effectively integrated information about reliability when making counterfactual judgments. Whether Carolyn was guessing or exercising her ability, when she was highly reliable, participants answered that it was significantly more likely that she would judge correctly in slightly different counterfactual circumstances.[93]

The proto-reliabilist hypothesis predicts, at the very least, that people will attribute knowledge only if they also attribute resistance. The proto-reliabilist hypothesis also predicts that people will attribute resistance only for reliably produced belief. If the more ambitious claims of some reliabilists are true, then when focusing on cases of true belief, we should also observe a strong positive correlation between knowledge judgments and resistance judgments, and perhaps we will even find evidence that resistance judgments cause or explain knowledge judgments.

To analyze the results, for each participant I calculated a knowledge score in the same way described in earlier experiments. I also calculated a resistance score similarly (“No” scored as +1, “Yes” scored as -1, multiplied by reported confidence, 1–6). Higher resistance scores indicate greater resistance to making a mistake.

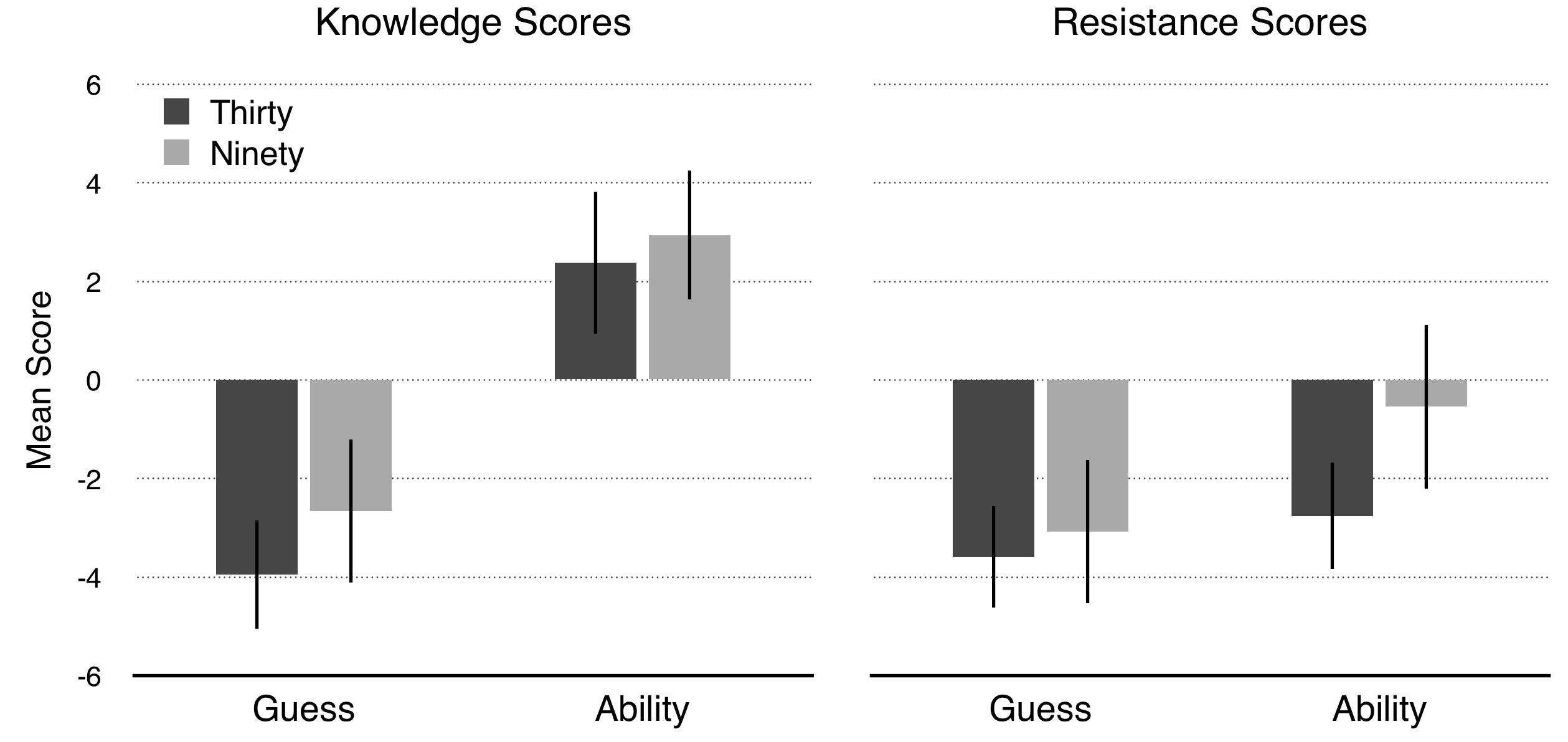
The proto-reliabilist predictions turned out false. Assignment to condition significantly affected knowledge scores.[94] There was a large main effect of Source,[95] no effect of Percent,[96] and no interaction.[97] Knowledge scores did not differ between Thirty Ability and Ninety Ability,[98] and they were significantly above the neutral midpoint (= 0) in each of those two conditions.[99] Knowledge scores did not differ between Thirty Guess and Ninety Guess,[100] and they were significantly below the midpoint in each of those two conditions.[101] Knowledge scores were significantly higher in Thirty Ability than Thirty Guess,[102] and they were higher in Ninety Ability than Ninety Guess.[103]

Assignment to condition significantly affected resistance scores.[104] There were small main effects of Source[105] and Percent[106] and no interaction.[107] Resistance scores were higher in Ninety Ability than in Thirty Ability,[108] and they were no different between Ninety Guess and Thirty Guess.[109] Resistance scores were below the midpoint in all four conditions, significantly so for Thirty Ability, Thirty Guess, and Ninety Guess.[110]

Overall, knowledge scores and resistance scores were moderately positively correlated.[111] Critically, knowledge scores were significantly higher than resistance scores in Thirty Ability[112] and Ninety Ability.[113] Also critically, even though knowledge scores were much higher in Thirty Ability than Thirty Guess, resistance scores in the two conditions didn’t differ.[114]

Figure 9. Experiment 9: Left panel: mean knowledge scores, derived for each participant by multiplying their dichotomous answer (scored +1 for “knows”, -1 for “only thinks”) by their reported confidence (1 = “not at all confident” to 6 = “completely confident”). Right panel: mean resistance scores, derived for each participant by multiplying their dichotomous answer (scored +1 for “No”, -1 for “Yes”) by their reported confidence. Scales ran from -6 to +6. Error bars represent bootstrapped 95% confidence intervals.

11. Conclusion

The view that knowledge must be reliably produced, knowledge reliabilism, is extremely popular in contemporary philosophy. But its popularity is due to inconclusive arguments and recently it has been challenged on theoretical grounds. Some have speculated that reliabilism draws support from the ordinary concept of knowledge and patterns in ordinary judgments about knowledge. That is, some have speculated that “commonsense” or “folk” epistemology is implicitly a form of proto-reliabilism and that reliabilist epistemology merely “explicates the ordinary standards” that guide knowledge judgments. This paper reported nine experiments designed to test the proto-reliabilist hypothesis.

The results show that the hypothesis is false. Folk epistemology fully embraces the possibility of unreliable knowledge. Multiple times I observed knowledge attributions reach 80–90% in cases of unreliably produced true belief. Participants consistently attributed knowledge to reliable and unreliable believers at similar rates. Participants attributed knowledge despite actively classifying the knower as unreliable, and they overwhelmingly declined to attribute knowledge in closely matched controls. More generally, although people understand and process explicit information about reliability, they do not seem to consult this information when making knowledge judgments. I observed the same basic pattern using different dependent measures (scaled and dichotomous), across different cover stories (computerized tests and ordinary tasks), for male and female believers, and for different faculties (vision and memory). None of this would happen if reliabilism was in sync with commonsense epistemology.

Reliabilists have also mischaracterized the “fundamental” intuitive relationship between knowledge and luck (e.g., Heller 1999; Lewis 1996; Dretske 1981; Pritchard 2005; see also Hetherington 2013). Almost no one thinks that knowledge is attributable to luck rather than ability, and it appears that people’s judgments about luck and ability guide their knowledge judgments, so commonsense does endorse an “anti-luck” intuition (Pritchard 2013). But most people do not share the intuition that reliability specifically is what rules out epistemically problematic luck.[115] Instead, a better candidate for capturing the intuitive relationship is that ability, reliable or unreliable, is what rules out luck.[116] At the same time, a nontrivial minority denied knowledge despite attributing true belief to ability, albeit a fairly unreliable one that produces false beliefs seventy percent of the time. This suggests that there are important individual differences in how much unreliability is viewed as consistent with knowledge or, perhaps more fundamentally, having an ability. Future work could investigate what these differences are and whether philosophers tend to have traits that predict greater intolerance of unreliability (compare Feltz & Cokely 2012). The present results suggest that neither gender nor age contributes to this intolerance in a consistent or meaningful way.

Reliabilists have also mischaracterized the intuitive relationship among reliability, knowledge, and counterfactual judgments. I studied two types of counterfactual judgments: judgments of adherence to the truth and resistance to error in close counterfactual circumstances. On the one hand, while the present results are consistent with the hypothesis that knowledge implies adherence in folk epistemology, I found that reliability is not essential to adherence. Instead, forming a true belief through unreliable ability brings with it enough adherence for knowledge. Moreover, it does not appear that people make knowledge judgments because of their adherence judgments—that is, people do not base their knowledge judgments on adherence judgments. However, I emphasize that this causal claim is preliminary and more work is needed before drawing firm conclusions.

On the other hand, I found evidence that resistance is not viewed as a requirement of knowledge. Instead, people attributed knowledge despite recognizing that the knower easily might have made a mistake. Prior research has found that people are willing to attribute knowledge while acknowledging that “there is at least some chance, no matter how small” that the person was wrong (Turri & Friedman 2014). The present findings on “might”-counterfactuals, and unreliably produced knowledge more generally, deepen our appreciation for the depth of fallibilist sentiment in folk epistemology. At this point, any form of infallibilism about knowledge should be viewed as radically revisionary and, consequently, should bestow significant advantages before being taken seriously. This pertains to views that require some form of unrestricted infallibility (as suggested, for example, by BonJour 2010 and Unger 1975), as well as “contextualist” or “relevant alternative” approaches that require infallibility relative to some restricted set of possibilities (as suggested by Dretske 1970; Stine 1976; Goldman 1976; Unger 1984; Cohen 1988; DeRose 1992; DeRose 1995; Lewis 1996; Cohen 2013).

I found two small pieces of evidence of reliabilist sentiment in folk epistemology, but this evidence raises more questions than it answers. On the one hand, in Experiment 2, reliability significantly boosted knowledge attributions in cases of false belief to chance rates (~40% compared to ~10% in cases of unreliably formed false belief). This puzzling finding could have been an anomaly; it did not replicate in Experiments 3–5. On the other hand, in Experiment 8, reliability significantly boosted knowledge attributions in cases where the person just guesses the correct answer (~30% compared to ~10% in cases where the person who just guesses the correct answer is unreliable). Again, this puzzling finding could have been an anomaly; it did not occur in Experiments 7 or 9. But even if these small and counterintuitive results turn out to be robust, in no way do they vindicate the proto-reliabilist hypothesis. Indeed, reliabilists might risk some embarrassment by touting them.

Some philosophers have wondered about our tendency in ordinary settings to count someone as knowing when all we know is that he has a true belief. For instance, some authors note that knowledge is “epistemically richer” than true belief and proceed to deny that our tendencies reveal that we ordinarily think of knowledge as mere true belief (Sripada & Stanley 2012: 7, discussing an example due to Hawthorne 2000). These authors hypothesize that “the folk are so easily led to mistake . . . true belief for knowledge” because, in many contexts, “all we care about” is that the “known” claim is true. In other words, lack of concern leads the folk to grant knowledge. But the findings from Experiment 7 suggest a completely different and more charitable explanation of any such tendency: when someone forms a true belief and has a cognitive ability relevant to acquiring the truth, the default assumption is that she formed the true belief through ability and thus knows.

The results also suggest an explanation for a recent development that has surprised many philosophers. For decades philosophers claimed that, intuitively, agents in “fake barn” cases lack knowledge (e.g., Goldman 1976; Sosa 1991: 238–9; Pritchard 2005: 161–2; Kvanvig 2008: 274). In a fake barn case, the agent (“Henry” in the original) perceives an object (a barn in the original) and this perceptual relation remains intact throughout. It is then revealed that the agent currently inhabits an environment filled with numerous fakes (“papier-mâché facsimiles of barns” in the original), which look like real ones. In an effort to explain why we are “strongly inclined” to deny knowledge in such cases, philosophers appeal to the agent’s high likelihood of forming a false belief in the context (Goldman 1976: 773; Pritchard 2014: Chapter 6; Plantinga 1993: 33).

But such “explanations” are idle if the tendency does not exist. And recent research has shown that in fact the tendency does not exist. Instead, people tend to attribute knowledge in fake-barn cases (Colaco, Buckwalter, Stich & Machery 2014). More generally in cases where an agent perceives something that makes her belief true and this perceptual relation remains intact, people overwhelmingly attribute knowledge, even when lookalikes pose a salient threat to the truth of the agent’s belief (Turri, Buckwalter & Blouw 2014; see also Turri in press b; Turri in press c). Indeed, commonsense views these similarly to paradigm instances of knowledge, with rates of knowledge attribution often exceeding 80%—which closely resembles the rate of unreliable knowledge attribution repeatedly observed in the present experiments. The present results thus suggest that philosophers were wrong about fake barn cases for the same reason that they were wrong about reliabilism: they assumed that knowledge requires reliability.

There is a view that coherently and elegantly unites all of these findings: abilism. Abilism defines knowledge as true belief manifesting the agent’s cognitive ability or powers.[117] Crucially, cognitive abilities can be unreliable in the sense that they needn’t produce true beliefs more often than not. Perhaps they need only produce true beliefs at rates exceeding chance. In fake barn cases and in the cases studied here, the agent is best interpreted as forming or retaining a true belief through cognitive ability (vision or memory). Thus he is best interpreted as knowing, which explains the extremely high rates of knowledge attribution. Moreover, as discussed in the Introduction, abilism can explain Goldman’s initial observations intended to motivate reliabilism. (For further ways that abilism co-opts reliabilism’s explanatory exploits, see Turri 2012.) Additionally, abilism is well suited to explain the present findings on epistemic luck and the enormous difference in knowledge judgments between the Ability and Guess conditions from Experiment 7, and the large differences between the Thirty Ability and Thirty Guess conditions in Experiments 8 and 9. Abilism is also fully consistent with the findings on the relationship between knowledge and counterfactual judgments.

Before concluding, I should note a potentially important limitation of the present findings and the recent findings on fake barn cases. All the cases tested involve beliefs that are naturally interpreted as non-inferential, relatively “immediate” beliefs based on perception and memory (Goldman 2008). But cognitive scientists have recently discovered many important qualitative differences in how inferential and non-inferential beliefs are evaluated (Turri & Friedman 2014; Turri 2015c; Turri 2015d; Zamir, Rito & Teichman in press; see also Pillow 1989; Sodian & Wimmer 1987). Further work could investigate whether inferential knowledge specifically requires reliability or interacts differently with judgments about luck. Relatedly, further work could also investigate whether the bar is set much higher for the possession of inferential cognitive abilities (discovering truths through reasoning) than for non-inferential cognitive abilities (e.g. perceptually detecting truths and retaining them through memory). Perhaps the intuitions motivating reliabilism are keyed to inferential knowledge or cognitive abilities, and philosophers mistakenly generalized this to cover all knowledge or cognitive abilities.

Regardless of what might be discovered about inferential knowledge specifically, the present findings constitute another exhibit in the mounting case against knowledge reliabilism, which is currently endorsed by almost all epistemologists. We have passed the point where it is reasonable to assume that reliabilism is true. Indeed, quite the opposite—moving forward, we should assume that reliabilism is false. Potent theoretical and empirical considerations have converged to support the conclusion that unreliable knowledge is not only possible but actual and widely recognized as perfectly ordinary. A new day has dawned. It’s time for the discipline to wake from its reliabilist slumber.

Acknowledgments

For helpful feedback and discussion, I thank Wesley Buckwalter, A.Y. Daring, Sandra DeVries, Ori Friedman, John Greco, Ashley Keefner, Josh Knobe, Janet Michaud, Blake Myers, Shaylene Nancekivell, Luis Rosa, David Rose, Jamie Sewell, Angelo Turri, and Sara Weaver. Thanks also to an audience at the 2014 Buffalo Experimental Philosophy Conference and participants in my 2014–15 seminar on experimental philosophy at the University of Waterloo. This research was supported by the Social Sciences and Humanities Research Council of Canada and an Early Researcher Award from the Ontario Ministry of Economic Development and Innovation.

References

• Alexander, Joshua (2012). Experimental Philosophy. Polity.
• Alston, William P. (1988). An Internalist Externalism. Synthese, 74(3), 265–283. http://dx.doi.org/10.1007/BF00869630
• Alston, William P. (1993). The Reliability of Sense Perception. Cornell University Press.
• Alston, William P. (1995). How to Think about Reliability. Philosophical Topics, 23(1), 1–29. http://dx.doi.org/10.5840/philtopics199523122
• Armstrong, David M. (1973). Belief, Truth and Knowledge. Cambridge University Press. http://dx.doi.org/10.1017/cbo9780511570827
• Austin, John L. (1956). A Plea for Excuses. Proceedings of the Aristotelian Society, 57, 1–30. http://dx.doi.org/10.1093/aristotelian/57.1.1
• Becker, Kelly (2006). Reliabilism and Safety. Metaphilosophy, 37(5), 691–704. http://dx.doi.org/10.1111/j.1467-9973.2006.00452.x
• Beebe, James R. (2012). Experimental Epistemology. In Andrew Cullison (Ed.), Continuum Companion to Epistemology (248–269). Continuum.
• Beebe, James R. (Ed.) (2014). Advances in Experimental Epistemology. Bloomsbury Academic.
• BonJour, Laurence (2002). Epistemology: Classic Problems and Contemporary Responses. Rowman & Littlefield.
• BonJour, Laurence (2010). The Myth of Knowledge. Philosophical Perspectives, 24(1), 57–83. http://dx.doi.org/10.1111/j.1520-8583.2010.00185.x
• Cohen, Stewart (1984). Justification and Truth. Philosophical Studies, 46(3), 279–295. http://dx.doi.org/10.1007/BF00372907
• Cohen, Stewart (2002). Basic Knowledge and the Problem of Easy Knowledge. Philosophy and Phenomenological Research, 65(2), 309–329. http://dx.doi.org/10.1111/j.1933-1592.2002.tb00204.x
• Cohen, Stewart (2013). Contextualism Defended. In Matthias Steup, John Turri, and Ernest Sosa (Eds.), Contemporary Debates in Epistemology (2nd ed., 69–75). Wiley-Blackwell.
• Colaco, David, Wesley Buckwalter, Stephen Stich, and Edouard Machery (2014). Epistemic Intuitions in Fake-Barn Thought Experiments. Episteme, 11(2), 199–212. http://dx.doi.org/10.1017/epi.2014.7
• Comesaña, Juan (2010). Evidentialist Reliabilism. Noûs, 44(4), 571–600. http://dx.doi.org/10.1111/j.1468-0068.2010.00748.x
• Comesaña, Juan (2002). The Diagonal and the Demon. Philosophical Studies, 110(2), 249–266. http://dx.doi.org/10.1023/A:1020656411534
• Craig, Edward (1990). Knowledge and the State of Nature: An Essay in Conceptual Synthesis. Oxford University Press.
• Cullen, Simon (2010). Survey-Driven Romanticism. Review of Philosophy and Psychology, 1(2), 275–296. http://dx.doi.org/10.1007/s13164-009-0016-1
• DeRose, Keith (1992). Contextualism and Knowledge Attributions. Philosophy and Phenomenological Research, 52(4), 913–929. http://dx.doi.org/10.2307/2107917
• DeRose, Keith (1995). Solving the Skeptical Problem. The Philosophical Review, 104(1), 1–52. http://dx.doi.org/10.2307/2186011
• Dretske, Fred (1971). Conclusive Reasons. Australasian Journal of Philosophy, 49(1), 1–22. http://dx.doi.org/10.1080/00048407112341001
• Dretske, Fred (1970). Epistemic Operators. The Journal of Philosophy, 67(24), 1007–1023. http://dx.doi.org/10.2307/2024710
• Dretske, Fred (1981). Knowledge and the Flow of Information. MIT Press.
• Fantl, Jeremy and Matthew McGrath (2009). Knowledge in an Uncertain World. Oxford University Press. http://dx.doi.org/10.1093/acprof:oso/9780199550623.001.0001
• Feldman, Richard (2003). Epistemology. Prentice Hall.
• Feldman, Richard (2013). Justification is Internal. In Matthias Steup, John Turri, and Ernest Sosa (Eds.), Contemporary Debates in Epistemology (2nd ed., 337–350). Wiley-Blackwell.
• Feltz, Adam and Edward T. Cokely (2012). The Philosophical Personality Argument. Philosophical Studies, 161(2), 227–246. http://dx.doi.org/10.1007/s11098-011-9731-4
• Foley, Richard (1985). What's Wrong with Reliabilism? The Monist, 68(2), 188–202. http://dx.doi.org/10.5840/monist198568220
• Fumerton, Richard (2006). Epistemology. Blackwell.
• Goldman, Alvin I. (1976). Discrimination and Perceptual Knowledge. Journal of Philosophy, 73(20), 771–791. http://dx.doi.org/10.2307/2025679
• Goldman, Alvin I. (1979). What is Justified Belief? In George Pappas (Ed.), Justification and Knowledge (1–23). Reidel. http://dx.doi.org/10.1007/978-94-009-9493-5_1
• Goldman, Alvin I. (1986). Epistemology and Cognition. Harvard University Press.
• Goldman, Alvin I. (1993). Epistemic Folkways and Scientific Epistemology. Philosophical Issues, 3, 271–285. http://dx.doi.org/10.2307/1522948
• Goldman, Alvin I. (2008). Immediate Justification and Process Reliabilism. In Quentin Smith (Ed.), Epistemology: New Essays (63–82). Oxford University Press. http://dx.doi.org/10.1093/acprof:oso/9780199264933.003.0004
• Goldman, Alvin I. (2012). Reliabilism and Contemporary Epistemology. Oxford University Press. http://dx.doi.org/10.1093/acprof:oso/9780199812875.001.0001
• Goldman, Alvin I. and Erik J. Olsson (2009). Reliabilism and the Value of Knowledge. In Adrian Haddock, Alan Millar, and Duncan Pritchard (Eds.), Epistemic Value (19–41). Oxford University Press. http://dx.doi.org/10.1093/acprof:oso/9780199231188.003.0002
• Greco, John (2000). Putting Skeptics in Their Place: The Nature of Skeptical Arguments and Their Role in Philosophical Inquiry. Cambridge University Press. http://dx.doi.org/10.1017/cbo9780511527418
• Greco, John (2010). Achieving Knowledge: A Virtue-Theoretic Account of Epistemic Normativity. Cambridge University Press. http://dx.doi.org/10.1017/cbo9780511844645
• Greco, John (2013). Justification Is Not Internal. In Matthias Steup, John Turri, and Ernest Sosa (Eds.), Contemporary Debates in Epistemology (2nd ed., 325–336). Wiley-Blackwell.
• Hawthorne, John (2000). Implicit Belief and A Priori Knowledge. The Southern Journal of Philosophy, 38(S1), 191–210. http://dx.doi.org/10.1111/j.2041-6962.2000.tb00937.x
• Hawthorne, John (2004). Knowledge and Lotteries. Oxford University Press.
• Hayes, Andrew F. (2013). Introduction to Mediation, Moderation, and Conditional Process Analysis: A Regression-Based Approach. Guilford Press.
• Heller, Mark (1995). The Simple Solution to the Problem of Generality. Noûs, 29(4), 501–515. http://dx.doi.org/10.2307/2216284
• Heller, Mark (1999). The Proper Role for Contextualism in an Anti-Luck Epistemology. Philosophical Perspectives, 13, 115–129. http://dx.doi.org/10.1111/0029-4624.33.s13.5
• Hetherington, Stephen (2013). There Can Be Lucky Knowledge. In Matthias Steup, John Turri, and Ernest Sosa (Eds.), Contemporary Debates in Epistemology (2nd ed., 164–176). Wiley-Blackwell.
• Hill, Christopher S. (1996). Process Reliabilism and Cartesian Scepticism. Philosophy and Phenomenological Research, 56(3), 567–581. http://dx.doi.org/10.2307/2108383
• Kornblith, Hilary (2002). Knowledge and its Place in Nature. Oxford University Press. http://dx.doi.org/10.1093/0199246319.001.0001
• Kvanvig, Jonathan (2008). Epistemic Luck. Philosophy and Phenomenological Research, 77(1), 272–281. http://dx.doi.org/10.1111/j.1933-1592.2008.00187.x
• Lehrer, Keith (1990). Theory of Knowledge. Westview Press.
• Lehrer, Keith (1997). Self-Trust. Oxford University Press. http://dx.doi.org/10.1093/acprof:oso/9780198236658.001.0001
• Lehrer, Keith and Stewart Cohen (1983). Justification, Truth, and Coherence. Synthese, 55(2), 191–207. http://dx.doi.org/10.1007/BF00485068
• Lewis, David (1996). Elusive Knowledge. Australasian Journal of Philosophy, 74(4), 549–567. http://dx.doi.org/10.1080/00048409612347521
• Nozick, Robert (1981). Philosophical Explanations. Harvard University Press.
• Pinillos, Nestor Ángel (2011). Some Recent Work in Experimental Epistemology. Philosophy Compass, 6(10), 675–688. http://dx.doi.org/10.1111/j.1747-9991.2011.00440.x
• Plantinga, Alvin (1993). Warrant and Proper Function. Oxford University Press. http://dx.doi.org/10.1093/0195078640.001.0001
• Pritchard, Duncan (2005). Epistemic Luck. Oxford University Press. http://dx.doi.org/10.1093/019928038x.001.0001
• Pritchard, Duncan (2009). Apt Performance and Epistemic Value. Philosophical Studies, 143(3), 407–416. http://dx.doi.org/10.1007/s11098-009-9340-7
• Pritchard, Duncan (2012). Anti-Luck Virtue Epistemology. Journal of Philosophy, 109(3), 247–279. http://dx.doi.org/10.5840/jphil201210939
• Pritchard, Duncan (2013). Knowledge Cannot be Lucky. In In Matthias Steup, John Turri, and Ernest Sosa (Eds.), Contemporary Debates in Epistemology (2nd ed., 152–164). Wiley-Blackwell
• Pritchard, Duncan (2014). What is this Thing Called Knowledge? (3rd ed.). Routledge.
• Riggs, Wayne D. (2002). Reliability and the Value of Knowledge. Philosophy and Phenomenological Research, 64(1), 79–96. http://dx.doi.org/10.1111/j.1933-1592.2002.tb00143.x
• Rose, David and Shaun Nichols (2013). The Lesson of Bypassing. Review of Philosophy and Psychology, 4, 599–619. http://dx.doi.org/10.1007/s13164-013-0154-3
• Rose, David, Jonathan Livengood, Justin Sytsma, and Edouard Machery (2012). Deep Trouble for the Deep Self. Philosophical Psychology, 25(5), 629–646. http://dx.doi.org/10.1080/09515089.2011.622438
• Roush, Sherrilyn (2005). Tracking Truth. Oxford University Press. http://dx.doi.org/10.1093/0199274738.001.0001
• Russell, Bertrand (2012). Human knowledge: Its Scope and Limits. Routledge.
• Sartwell, Crispin (1992). Why Knowledge is Merely True Belief. The Journal of Philosophy, 89(4), 167–180. http://dx.doi.org/10.2307/2026639
• Sellars, Wilfrid (1963). Science, Perception and Reality. Ridgeview Publishing Company.
• Sosa, Ernest (1991). Knowledge in Perspective. Cambridge University Press. http://dx.doi.org/10.1017/cbo9780511625299
• Sosa, Ernest (1999). How to Defeat Opposition to Moore. Philosophical Perspectives, 13, 141–153. http://dx.doi.org/10.1111/0029-4624.33.s13.7
• Sosa, Ernest (2007). A Virtue Epistemology: Apt Belief and Reflective Knowledge (Vol. 1). Oxford University Press. http://dx.doi.org/10.1093/acprof:oso/9780199297023.001.0001
• Sripada, Chandra S. and Jason Stanley (2012). Empirical Tests of Interest-Relative Invariantism. Episteme, 9(1), 3–26. http://dx.doi.org/10.1017/epi.2011.2
• Stanley, Jason (2005). Knowledge and Practical Interests. Oxford University Press. http://dx.doi.org/10.1093/0199288038.001.0001
• Starmans, Christina and Ori Friedman (2012). The folk conception of knowledge. Cognition, 124(3), 272–283. http://dx.doi.org/10.1016/j.cognition.2012.05.017
• Cohen, Stewart (1988). How to Be a Fallibilist. Philosophical Perspectives, 2, 91–123. http://dx.doi.org/10.2307/2214070
• Stine, Gail C. (1976). Skepticism, Relevant Alternatives, and Deductive Closure. Philosophical Studies, 29, 249–261. http://dx.doi.org/10.1007/BF00411885
• Stroud, Barry (1984). The Significance of Philosophical Skepticism. Clarendon Press. http://dx.doi.org/10.1093/0198247613.001.0001
• Swain, Marshall (1981). Reasons and Knowledge. Cornell University Press.
• Swain, Stacey, Joshua Alexander, and Jonathan M. Weinberg (2008). The Instability of Philosophical Intuitions: Running Hot and Cold on Truetemp. Philosophy and Phenomenological Research, 84(1), 138–155. http://dx.doi.org/10.1111/j.1933-1592.2007.00118.x
• Turri, John (2011). The Express Knowledge Account of Assertion. Australasian Journal of Philosophy, 89(1), 37–45. http://dx.doi.org/10.1080/00048401003660333
• Turri, John (2012). Review of: Achieving Knowledge: A Virtue-Theoretic Account of Epistemic Normativity, by John Greco. Mind, 121(481), 183–187. http://dx.doi.org/10.1093/mind/fzs032
• Turri, John (2013). A Conspicuous Art: Putting Gettier to the Test. Philosophers' Imprint, 13(10), 1–16.
• Turri, John (2014). The Problem of ESEE Knowledge. Ergo, 1(4), 101–127. http://dx.doi.org/10.3998/ergo.12405314.0001.004
• Turri, John (2015a). Unreliable Knowledge. Philosophy and Phenomenological Research, 90(3), 529–545.
• Turri, John (2015b). From Virtue Epistemology to Abilism: Theoretical and Empirical Developments. In Christian B. Miller, R. Michael Furr, Angela Knobel, and William Fleeson (Eds.), Character: New Directions from Philosophy, Psychology, and Theology (315–330). Oxford University Press.
• Turri, John (2015c). An Open and Shut Case: Epistemic Closure in the Manifest Image. Philosophers' Imprint, 15(2), 1–18.
• Turri, John (2015d). Skeptical Appeal: The Source-Content Bias. Cognitive Science, 39(2), 307–324. http://dx.doi.org/10.1111/cogs.12153
• Turri, John (in press a). Primate Social Cognition and the Core Human Knowledge Concept. In Eric McCready, Masaharu Mizumoto, Jason Stanley, and Stephen Stich (Eds.), Epistemology for the Rest of the World: Linguistic and Cultural Diversity and Epistemology. Oxford University Press.
• Turri, John (in press b). Knowledge and Assertion in “Gettier” Cases. Philosophical Psychology.
• Turri, John (in press c). Vision, Knowledge, and Assertion. Consciousness and Cognition.
• Turri, John and Ori Friedman. (2014). Winners and Losers in the Folk Epistemology of Lotteries. In James R. Beebe (Ed.), Advances in Experimental Epistemology (45–70). Continuum.
• Turri, John, Wesley Buckwalter, and Peter Blouw. (2014). Knowledge and luck. Psychonomic Bulletin & Review, 22(2), 378–390. http://dx.doi.org/10.3758/s13423-014-0683-5
• Unger, Peter (1975). Ignorance: A Case for Skepticism. Oxford University Press.
• Unger, Peter (1984). Philosophical Relativity. Oxford University Press.
• Vogel, Jonathan (1990). Are There Counterexamples to the Closure Principle? In Michael D. Roth and Glenn Ross (Eds.), Philosophical Studies Series (Vol. 48, 13–27). Springer. http://dx.doi.org/10.1007/978-94-009-1942-6_2
• Vogel, Jonathan. (2000). Reliabilism Leveled. The Journal of Philosophy, 97(11), 602–623. http://dx.doi.org/10.2307/2678454
• Weinberg, Jonathan M., Shaun Nichols, and Stephen Stich (2001). Normativity and Epistemic Intuitions. Philosophical Topics, 29(1–2), 429–460. http://dx.doi.org/10.5840/philtopics2001291/217
• Williamson, Timothy (2000). Knowledge and its Limits. Oxford University Press.
• Zagzebski, Linda T. (1996). Virtues of the Mind: An Inquiry into the Nature of Virtue and the Ethical Foundations of Knowledge. Cambridge University Press. http://dx.doi.org/10.1017/cbo9781139174763
• Zamir, Eyal, Ilana Ritov, and Doran Teichman (in press). Seeing is Believing: The Anti-Inference Bias. Indiana Law Journal. http://dx.doi.org/10.2139/ssrn.1989561

Notes

1. Goldman’s discussion pertains to justification explicitly, but he also says that justification is necessary for knowledge (Goldman 1979: 340). Other writers reject the connection between justification and reliability but accept Goldman’s view about the relationship between knowledge and reliability (e.g., Feldman 2003: 90ff; Fumerton 2006: 86ff).

2. Although Craig eschews the project of identifying necessary and sufficient conditions for the application of our ordinary knowledge concept, he also suggests that a good account of the concept will come close to fitting that format (1990: 5). For further discussion of the shortcomings of Craig’s intriguing view, see Turri (in press a).

3. Aged 18–66 years, mean age = 32 years; 96% reporting English as a native language; 49 female. Participants were recruited and tested online (using Amazon Mechanical Turk and Qualtrics) and compensated $0.35 for approximately 2 minutes of their time. Repeat participation was prevented. Eleven participants failed comprehension questions, but excluding them from the analysis does not affect the results reported below, so I retained their data to increase statistical power in this first study.

4. Calculated using the software application G*Power v. 3.1.5 (Faul, Erdfelder, Lang & Axel 2007). The calculation assumed a mean difference of 1, a common standard deviation of 1, and the conventional beta and alpha levels of .20 and .05.

5. Post hoc power analysis revealed that the test’s power to detect a mean difference of 1 was .97, which indicates that it had a 97% chance of detecting the difference, if it exists. The calculation used the observed common standard deviation of 1.11 and a sample size of 36 per group. Post hoc power analysis also revealed that the test was sufficiently powered to detect a mean difference of 0.66, assuming the conventional beta and alpha levels of .20 and .05.

6. ANOVA, F(2, 110) = 67.93, p < .001, η_p2 = .553. An initial omnibus ANOVA revealed no main or interaction effects for participant age: 2 equal groups, cut-point = 28 years; F(1, 79) = 0.68, p = .412) and no interaction effects for participant gender. However, it did indicate a main effect for participant gender, whereby women were more inclined to attribute knowledge than men, M = 4.27/3.77, SD = 1.91/1.98: gender, F(1, 110) = 5.48, p = .021, η_p2 = .051. However, a follow-up independent samples t-test did not detect a gender difference, t(111) = -1.348, p = .180, MD = 0.50 [-1.23, 0.24]; a nonparametric Mann-Whitney U test detected no difference either, U(113) = 1306, Z = -1.57, p = .117. Moreover, this gender-effect is not replicated in any other study reported here, which suggests that it might be a false positive (type I error): caution is warranted.

7. False/Ten/Ninety: M = 2.07/4.86/5.27, SD = 1.65/1.3/0.84. Independent samples t-test comparing False and Ten, t(74) = -8.05, p < .001, MD = -2.78 [-3.47, -2.10]. Independent samples t-test comparing False and Ninety, t(60.7) = -10.615, p < .001, MD = -3.20 [-3.78, -2.61].

8. Independent samples t-test, t(70) = -1.60, p = .113, MD = -0.41 [-0.93, 0.10].

9. Aged 18–72 years, mean age = 33 years; 94% reporting English as a native language; 42 female. I excluded data from nineteen participants who failed comprehension questions, but including them does not affect the results reported below.

10. Participants also rated their confidence in their answer to the dichotomous knowledge probe. Combining the dichotomous response with reported confidence resulted in the same pattern of results as for the dichotomous response alone, so I omit discussion of it.

11. Preliminary analyses revealed no effect of participant age or gender on knowledge judgments.

12. Fisher’s exact test, p = .318.

13. Chi-square goodness of fit test, χ²(1, 28) = 7.00, p = .008.

14. Chi-square goodness of fit test, χ²(1, 30) = 16.13, p < .001.

15. Chi-square goodness of fit test, χ²(1, 31) = 1.58, p = .209.

16. However, also compare the finding in Experiment 6, where increased reliability made it more likely that people attribute knowledge to someone who “just guesses” the correct answer.

17. Fisher’s exact test, p = .04, Cramer’s V = .288.

18. True Ten/True Ninety: M = 2.54/5.25, SD = 1.69/0.57. Independent samples t-test, t(32.3) = -8.12, p < .001, MD = -2.71 [-3.39, -2.03].

19. One sample t-tests. True Ten: t(27) = -3.02, p = .005, MD = -0.96 [-1.62, -0.31]. True Ninety: t(31) = 17.43, p < .001, MD = 1.75 [1.55, 1.95].

20. M = 2.48, SD = 1.63. One sample t-test, t(20) = -2.88, p = .009, MD = -1.02 [-1.77, -0.28].

21. Attribute/Deny: M = 2.48/2.71, SD = 1.63/1.98. Independent samples t-test, t(26) = 0.32, p = .753, MD = 0.24 [-1.30, 1.78].

22. Aged 19–67 years, mean age = 34 years; 94% reporting English as a native language; 55 female.

23. Preliminary analyses revealed no effect of participant age or gender on knowledge judgments.

24. Fisher’s exact test, p = 1.

25. Chi-square goodness of fit test, χ²(1, 31) = 7.26, p = .007.

26. Chi-square goodness of fit test, χ²(1, 30) = 13.33, p < .001.

27. Fisher’s exact test, p = .561.

28. True Ten/True Ninety: M = 2.94/5.26, SD = 1.73/0.73. Independent samples t-test, t(40.32) = -6.89, p < .001, MD = -2.32 [-3.00, -1.64].

29. One sample t-tests. True Ten: t(30) = -1.82, p = .079, MD = -0.57 [-1.20, 0.07]. True Ninety: t(30) = 13.43, p < .001, MD = 1.76 [1.49, 2.03].

30. M = 2.65, SD = 1.75. One sample t-test, t(22) = -2.33, p = .030, MD = -0.85 [-1.60, -0.09].

31. Attribute/Deny: M = 2.65/3.75, SD = 1.75/1.49. Independent samples t-test, t(29) = 1.58, p = .124, MD = -1.10 [-0.32, 2.52].

32. Aged 18–72 years, mean age = 33 years; 94% reporting English as a native language; 42 female. I excluded data from nineteen participants who failed comprehension questions, but including them does not affect the results reported below.

33. Fisher’s exact test, p = 1.

34. Chi-square goodness of fit test, χ²(1, 36) = 18.78, p < .001.

35. Fisher’s exact test, p = .429.

36. Chi-square goodness of fit tests. Unreliable False: χ²(1, 33) = 25.49, p < .001. Reliable False: χ²(1, 35) = 17.86, p < .001.

37. Unreliable False/Reliable False: M = 1.73/2.94, SD = 1.26/1.41; independent samples t-test, t(66) = -3.74, p < .001, MD = -1.22 [-1.87, -0.57]. Unreliable True/Reliable True: M = 2.17/5.56, SD = 1.3/0.71; independent samples t-test, t(54.6) = -13.69, p < .001, MD = -3.39 [-3.89, -2.90].

38. One sample t-test, t(30) = -4.94, p < .001, MD = -1.77 [-1.66, -0.69].

39. Knows/only thinks: M = 2.32/1.20, SD = 1.3/0.45. Independent samples t-test, t(34) = 1.86, p = .072, MD = 1.12 [-0.11, 2.35].

40. An anonymous referee raised this alternative reading.

41. Aged 18–72 years, mean age = 33 years; 94% reporting English as a native language; 42 female. I excluded data from nineteen participants who failed comprehension questions, but including them does not affect the results reported below.

42. Fisher’s exact test, p = 1.

43. Chi-square goodness of fit test, χ²(1, 30) = 8.53, p = .003.

44. Fisher’s exact test, p = .671.

45. Chi-square goodness of fit tests. Unreliable False: χ²(1, 30) = 16.13, p < .001. Reliable False: χ²(1, 30) = 22.53, p < .001.

46. True Unreliable/True Reliable: M = 3.03/5.43, SD = 1.61/0.63. Independent samples t-test, t(37.60) = -7.62, MD = 2.40 [-3.04, -1.76].

47. One sample t-tests. True Unreliable: t(29) = -1.59, p = .123, MD = -0.47 [-1.07, 0.13]. True Reliable: t(29) = 16.91, p < .001, MD = 1.93 [1.70, 2.17].

48. Aged 19–69 years, mean age = 32 years; 97% reporting English as a native language; 54 female. Thirteen participants didn’t correctly answer the manipulation check correctly. But, as with every other experiment reported in this paper, excluding them from the analysis didn’t affect the pattern of results reported in the main text, so I retained their responses to increase statistical power.

49. Indicates paragraph break on the participant’s screen.

50. Ninety percent of participants correctly identified Carolyn’s level of reliability, chi-square goodness of fit test, χ²(1, 133) = 79.77, p < .001.

51. ANOVA, F(1, 129) = 91.01, p < .001, η_p2 = .414.

52. ANOVA, F(1, 129) = 0.30, p = .535, η_p2 = .003.

53. One sample t-tests: Thirty Ability, M = 3.00, SD = 4.28, t(31) = 3.97, p < .001, MD = 3.00 [1.46, 4.54]. Ninety Ability, M = 4.09, SD = 3.32, t(33) = 7.19, p < .001, MD = 4.09 [2.93, 5.24]. Thirty Guess, M = -2.85, SD = 4.37, t(32) = -3.74, p < .001, MD = -2.85 [-4.40, -1.30]. Ninety Guess, M = -3.09, SD = 3.70, t(33) = -4.86, p < .001, MD = -3.09 [-4.38, -1.80].

54. Independent samples t-test, t(65) = 0.24, p = .809, MD = 0.24 [-1.74, 2.21].

55. Independent samples t-test, t(58.4) = - 1.15, p = .255, MD = -1.09 [-2.98, 0.81].

56. Aged 18–72 years, mean age = 32 years; 97% reporting English as a native language; 89 female. I recruited a higher number of participants per condition this time mainly because I had no way of estimating the potential difference between Control and Ability, which I was interested in. So I doubled the participants per condition. As it turns out, the additional statistical power was inadequate to detect a significant difference between Control and Ability.

57. ANOVA, F(2, 223) = 50.95, p < .001, η_p2 = .314. An initial omnibus ANOVA revealed no main or interaction effects for participant age or gender: gender, F(1, 214) = 0.54, p = .464; age, F(1, 214) = 0.09, p = .771.

58. Control/Ability/Guess: M = 2.21/2.19/-3.58, SD = 4.20/4.37/3.60. Independent samples t-test comparing Control and Guess, t(145.14) = 9.10, p < .001, MD = 5.79 [4.54, 7.05]; comparing Ability and Guess, t(143.12) = 8.84, p < .001, MD = 5.76 [4.48, 7.05]. The effect size for the Ability/Guess comparison is extremely large: the eta squared statistic is .353, which indicates that over 35% of variance in knowledge judgments is explained by the difference between getting the truth through ability rather than luck.

59. Independent samples t-test, t(148) = 0.04, p = .970.

60. One sample t-tests: Control, t(74) = 4.57, p < .001, MD = 2.21 [1.25, 3.18]. Ability, t(74) = 4.37, p < .001, MD = 2.19 [1.18, 3.19]. Guess, t(75) = -8.66, p < .001, MD = -3.58 [-4.40, -2.76].

61. ANOVA, F(2, 223) = 77.51, p < .001, η_p2 = .41. An initial omnibus ANOVA revealed no main or interaction effects for participant age (two equal groups, cut-point = 29 years) or gender: gender, F(1, 214) = 0.09, p = .770; age, F(1, 214) = 0.58, p = .447.

62. Control/Ability/Guess: M = 4.61/4.28/-1.38, SD = 2.00/2.62/4.71. One sample t-tests: Control, t(74) = 19.92, p < .001, MD = 4.61 [4.15, 5.07]. Ability, t(74) = 14.16, p < .001, MD = 4.28 [3.68, 4.88]. Guess, t(75) = -2.56, p = .013, MD = -1.38 [-2.46, -0.31].

63. Pearson’s correlation, r = .622, N = 226, p < .001.

64. As determined by a bootstrap mediation analysis (Hayes 2013). Because knowledge scores and explanations scores were basically the same in the Control and Ability conditions, I first collapsed these into a single group (Ability*) for purposes of analysis. I then entered condition as the independent variable (dummy coded, Guess = 0, Ability* = 1), knowledge score as the dependent variable, and explanation score as the potential mediator: 95% CI for the indirect effect = 2.11 to 4.12; ratio of indirect to direct effect = 1.04, 95% CI = 0.53 to 2.94. The reverse mediation model—with condition as the independent variable, explanation score as the dependent variable, and knowledge score as the potential mediator—was also significant: 95% CI for the indirect effect = 1.38 to 2.73; ratio of indirect to direct effect = 0.51, 95% CI = 0.28 to 0.96. But I assume that the causal model presupposed by this latter mediation analysis is implausible. I will not pursue the matter further here.

65. Binary logistic regression, Beta = 3.645, SE = 0.62, Wald = 35.10, df = 1, p < .001, odds ratio = 38.33 [11.47, 128.13]. The model contained answer to the dichotomous explanation probe as the predictor and answer to the dichotomous knowledge probe as the outcome. The model was statistically significant, χ²(1, N = 226) = 77.59, explained between 29.1% and 38.8% of the variance in knowledge attribution, and correctly classified 75% of cases.

66. “Adherence” is Nozick’s (1981: 212) term. I find it especially apt.

67. Aged 18–70 years, mean age = 31 years; 95% reporting English as a native language; 52 female. Twenty participants failed a comprehension question, but excluding these participants doesn’t affect the pattern of results reported below.

68. ANOVA, F(3, 138) = 40.19, p < .001, η_p2 = .466. An initial omnibus ANOVA revealed no main or interaction effects for participant age or gender: gender, F(1, 134) = 1.38, p = .243; age (two equal groups, cut-point = 28 years), F(1, 134) = 1.41, p = .237.

69. ANOVA, F(1, 138) = 3.05, p = .083, η_p2 = .022.

70. ANOVA, F(1, 138) = 117.30, p < .001, η_p2 = .459.

71. ANOVA, F(1, 138) = 1.35, p = .248.

72. M = 3.23/3.58, SD = 3.30/3.73. Independent samples t-test, t(69) = -0.424, p = .673, MD = -0.35 [-2.02, 1.31].

73. One sample t-tests. Thirty Ability: t(34) = 5.79, p < .001, MD = 3.23 [2.10, 4.36]. Ninety Ability: t(35) = 5.77, p < .001, MD = 3.58 [2.32, 4.87].

74. M = -2.27/-4.03, SD = 4.42/2.66, t(59.8) = -2.05, p = .045, MD = -1.76 [-3.47, -0.04]. The magnitude of the difference in means was medium (Cohen’s d = 0.52)

75. One sample t-tests: Thirty Guess, t(33) = -8.84, p < .001, MD = -4.03 [-4.96, -3.10]. Ninety Guess, t(36) = -3.12, p = .004, MD = -2.27 [-3.74, -0.80].

76. Independent samples t-test, t(67) = -10.05, p < .001, MD = 7.25 [5.82, 8.70]. The magnitude of the difference in means was extremely large (Cohen’s d = 2.46).

77. Independent samples t-test, t(69.6) = -6.12, p < .001, MD = 5.85 [3.95, 7.76]. The magnitude of the difference in means was extremely large (Cohen’s d = 1.46).

78. ANOVA, F(3, 138) = 14.24, p < .001, η_p2 = .236. An initial omnibus ANOVA revealed no main or interaction effects for participant age or gender.

79. ANOVA, F(1, 138) = 38.59, p < .001, η_p2 = .236.

80. ANOVA, F(1, 138) = 2.93, p = .089, η_p2 = .021.

81. ANOVA, F(1, 138) = 1.08, p = .300.

82. M = 2.89/4.75, SD = 3.61/1.98. Independent samples t-test, t(52.4) = -2.69, p = .010, MD = -1.86 [-3.26, -0.47]. The magnitude of the difference in means was large (Cohen’s d = .74).

83. One sample t-tests. Thirty Ability: t(34) = 4.73, p < .001, MD = 2.89 [1.65, 4.13]. Ninety Ability: t(35) = 14.42, p < .001, MD = 4.75 [4.08, 5.42].

84. Thirty/Ninety Guess, M = -0.62/-0.16, SD = 4.83/4.98. Independent samples t-test, t(69) = -0.39, p = .698, MD = 0.46 [-2.78, 1.87].

85. One sample t-tests. Thirty Guess: t(33) = 0.745, p = .462, MD = -0.62 [-2.31, 1.07]. Ninety Guess: t(36) = -0.198, p = .844, MD = -0.16 [-1.82, 1.50].

86. Independent samples t-test: t(61.05) = 3.4, p = .001, MD = 3.50 [1.44, 5.56]. The magnitude of the difference in means was large (Cohen’s d = 0.88).

87. Independent samples t-test: t(47.32) = 5.57, MD = 4.91 [3.34, 6.69]. The magnitude of the difference in means was extremely large (Cohen’s d = 1.62).

88. Pearson’s correlation, r = .37, N = 142, p < .001.

89. As determined by two separate bootstrap mediation analyses. Comparing Ninety Ability and Ninety Guess, I entered Source as the independent variable, knowledge score as the outcome, and adherence score as the potential mediator: 95% CI for the indirect effect = -1.32 to 1.49; ratio of indirect to direct effect = .001, 95% CI for ratio = -0.28 to 0.29. Using the same procedure to compare Thirty Ability and Thirty Guess, there was a very weak indirect effect = 0.47, 95% CI = 0.02 to 1.38; ratio of indirect to direct effect = 0.06, 95% CI = 0.00 to 0.20. As a point of further information, in a multiple regression model with knowledge score as the outcome and Source, Percent, and adherence scores as predictors (model fit, R² = .464), Source significantly predicted knowledge scores (Beta = .644, p < .001), but Percent (Beta = .101, p = .111) and adherence scores (Beta = .060, p = .402) did not.

90. A causal search with the Greedy Equivalence Search (GES) algorithm returned a model in which Source caused both knowledge judgments and adherence judgments, Percent caused neither judgment, and there was no causal connection between knowledge judgments and adherence judgments. The model fit the data well, χ²(4) = 6.74, p = .15, BIC = -13.08. The causal search was conducted with Tetrad 5 (http://www.phil.cmu.edu/projects/tetrad/). GES considers all possible models available given the different variables. Each variable is treated as a node. GES assigns an information score to the model in which all the nodes are disconnected—the “null model.” GES then evaluates adding causal arrows—“edges”—between the nodes. GES adds edges that best improve the model’s information score, if such edges exist, until adding more edges does not improve the information score. At this point, GES evaluates whether deleting any edges will further improve the information score, and it deletes any such edges. See Rose & Nichols 2013 and Rose, Livengood, Sytsma, & Machery 2012 for prior applications of GES to philosophical debates, as well as the literature cited therein for further details on the algorithm.

91. Aged 18–63 years, mean age = 31 years; 95% reporting English as a native language; 57 female.

92. In an attempt to detect subtler aspects of the potential relationship between reliability and knowledge judgments, I also collected reaction time data in this experiment. More specifically, I collected information on how long it took people to register their knowledge judgments. (The timing mechanism was invisible to participants and they were not told that they were being timed.) It could turn out that although people attribute reliable and unreliable knowledge at equal rates, reliability facilitates more rapid knowledge attribution, or unreliability facilitates more rapid knowledge denial. If this were true, then it might suggest that reliability is associated with prototypical knowledge, whereas unreliability is not. In this way, reliability might be importantly conceptually connected to knowledge without being a necessary condition on knowledge. This could explain why philosophers are so easily tempted by the false view that, as a matter of conceptual necessity, knowledge requires reliability. The explanation would be that philosophers have correctly sensed a conceptual connection but misidentified its nature. However, I found no evidence for this hypothesis, because it turned out that people recorded their knowledge judgments faster when the source of belief was more unreliable.

93. Independent samples t-test. Comparing Ninety Guess and Thirty Guess: M = 4.37/3.59, SD = 1.10/1.07, t(75) = 3.15, p = .002, MD = 0.78 [0.29, 1.27]. Comparing Ninety Ability and Thirty Ability: 4.97/3.76, SD = 1.04/0.99, t(67) = 4.94, p < .001, MD = 1.21 [0.72, 1.70]. One sample t-tests revealed that likelihood scores were significantly above the theoretical midpoint (= 3.5) in Ninety Guess, t(37) = 4.86, p < .001, and in Ninety Ability, t(34) = 8.35, p < .001. By contrast, likelihood scores did not differ from the midpoint in either Thirty Guess, t(38) = 0.52, p = .603, or Thirty Ability, t(33) = 1.57, p = .127.

94. ANOVA, F(3, 142) = 28.73, p < .001, η_p² = .378. An initial omnibus ANOVA revealed no main or interaction effects for participant age or gender: gender, F(1, 130) = 2.05, p = .155; age (two equal groups, cut-point = 29 years), F(1, 130) = 2.18, p = .142.

95. ANOVA, F(1, 142) = 83.42, p < .001, η_p² = .370.

96. ANOVA, F(1, 142) = 2.01, p = .159.

97. ANOVA, F(1, 142) = 0.313, p = .577.

98. Thirty/Ninety Ability, M = 2.38/3.94, SD = 4.14/3.81. Independent samples t-test, t(67) = -0.585, p = .560, MD = -0.56 [-2.47, 1.35].

99. One sample t-tests. Thirty Ability, t(33) = 3.354, p = .002, MD = 2.38 [0.93, 3.83]. Ninety Ability, t(34) = 4.57, p < .001, MD = 2.94 [1.63, 4.25].

100. Thirty/Ninety Guess, M = -3.95/-2.66, SD = 3.39/4.37. Independent samples t-test, t(69.8) = -1.45, p = .153, MD = -1.29 [-3.07, 0.49].

101. One sample t-tests. Thirty Guess, t(38) = -7.26, p < .001, MD = -3.95 [-5.05, -2.85]. Ninety Guess, t(37) = -3.75, p = .001, MD = -2.66 [-4.09, -1.22].

102. Independent samples t-test, t(63.93) = 7.08, p < .001, MD = 6.33 [4.54, 8.12]. The magnitude of the difference in means was extremely large (Cohen's d = 1.77).

103. Independent samples t-test, t(71) = 5.81, p < .001, MD = 5.60 [3.68, 7.52]. The magnitude of the difference in means was extremely large (Cohen’s d = 1.38).

104. ANOVA, F(3, 142) = 4.318, p = .006, η_p² = .084.

105. ANOVA, F(1, 142) = 6.82, p = .010, η_p² = .046.

106. ANOVA, F(1, 142) = 4.51, p = .036, η_p² = .031.

107. ANOVA, F(1, 142) = 1.77, p = .186.

108. Ninety/Thirty Ability, M = -0.54/-2.76, SD = 4.84/4.16. Independent samples t-test, t(66.02) = 2.05, p = .045, MD = 2.22 [0.06, 4.39]. The magnitude of the difference in means was medium (Cohen’s d = 0.50).

109. Ninety/Thirty Guess, M = -3.08/-3.59, SD = 3.27/3.16. Independent samples t-test, t(75) = -0.70, p = .488, MD = 0.51 [-0.95, 1.97].

110. One sample t-tests. Thirty Guess, t(38) = -7.09, p < .001, MD = -3.59 [-4.61, -2.57]. Thirty Ability, t(33) = -3.88, p < .001, MD = -2.76 [-4.22, -1.31]. Ninety Guess, t(37) = -5.81, p < .001, MD = -3.08 [-4.15, -2.01]. Ninety Ability, t(34) = -0.66, p = .512, MD = -0.54 [-2.21, 1.12].

111. Pearson’s correlation, r = .422, N = 146, p < .001.

112. Paired sample t-test, t(33) = 6.54, p < .001, MD = 5.14 [3.55, 6.75]. The magnitude of the difference in means was very large (Cohen’s d = 1.24).

113. Paired sample t-test, t(34) = 4.55, p < .001, MD = 3.49 [1.93, 5.04]. The magnitude of the difference in means was large (Cohen’s d = 0.80).

114. Independent samples t-test, t(71) = 0.96, p = .340, MD = 0.83 [-0.89, 2.54]. A causal search with the Greedy Equivalence Search (GES) algorithm returned a model in which Source was the sole cause of knowledge judgments, and knowledge judgments were the sole cause of resistance judgments. Resistance judgments and Percent conspired to cause counterfactual likelihood judgments (i.e., response to the manipulation check). The model fit the data well, χ²(6) = 9.55, p = .15, BIC = -20.35.

115. Here I use “reliable” as knowledge reliabilists do, namely, indicating success on the (vast) majority of trials (see the Introduction for references). For the record, while I don’t begrudge researchers adapting terminology to their own purposes, I question whether this corresponds to the ordinary meaning of “reliable” or is even the sense of “reliable” most relevant to assessing knowledge and other accomplishments. For more discussion, see Turri (2015a).

116. As argued elsewhere on theoretical grounds (Turri 2012; Turri 2015a). Some philosophers seem to have recognized that ability is what rules out luck, but they pair this with the mistaken view that ability requires reliability (e.g., Sosa 2007; Greco 2010; Pritchard 2012).

117. This is an approximate and simplified statement of the view. Fully spelled out, knowledge is approximately true thin belief manifesting cognitive power. For more on the motivation for these refinements, see Turri (2015b).