Partial Model Theory as Model Theory

Abstract

I show that the partial truth of a sentence in a partial structure is equivalent to the truth of that sentence in an expansion of a structure that corresponds naturally to the partial structure. Further, a mapping is a partial homomorphism/partial isomorphism between two partial structures if and only if it is a homomorphism/isomorphism between their corresponding structures. It is a corollary that the partial truth of a sentence in a partial structure is equivalent to the truth of a specific Ramsey sentence in a corresponding structure. Hence the partial structures approach can be expressed in standard first or second-order model theory, and it can be captured in the received view on scientific theories as developed by Carnap and Hempel.

1. Introduction

In an overview of the historical turn in the philosophy of science, Bird reports that

One dominant theme of this descriptive philosophy of science is the rejection of formal approaches. Van Benthem (1982: 432) explains that they are seen as “inappropriate, or, at best, inadequate (to the extent of being useless). The scientific reality one should be concerned with is either too ‘dynamic’, or too ‘complex’ to be captured by formal tools”. But this view has not been borne out. For, although formal approaches may not capture all complexities of the scientific endeavor, they are helpful in finding answers to a number of philosophical questions about science (Leitgeb 2011; van Benthem 2012) and are essential for finding others (Suppes 1968; Leitgeb 2011; Halvorson 2012: §7).

Of course, not every formal approach to the philosophy of science is bound to be useful, and it has become common lore that the logical empiricists’ approach (Carnap 1966; Hempel 1958), the so-called “received view”, can capture little (if anything) of science.[1] Da Costa and French (2003: 3) report “the continued unfolding of the post-positivist gulf between our actual knowledge-gathering activities and the philosophical characterization of these activities”, and van Fraassen states:

Alternative to the received view, van Fraassen (1989: Ch. 9) suggests the semantic approach, in which scientific theories are described as classes of model theoretic or set theoretic structures. This approach is considered much closer to actual scientific practice, despite being formal (see Muller 2010: 93–94). Lloyd (1988: §§3–4) argues that the semantic approach can be applied to non-formal theories with great success. Da Costa and French further suggest that through a generalization of model theoretic structures to partial structures and a corresponding generalization of the model theoretic notion of truth, the semantic approach can account for all complexities of the scientific endeavor in a unified way:

Da Costa and French (2000) take the resulting partial model theory to increase the expressive power of model theory significantly, and Le Bihan (2012: n. 3, §5) places the partial structure approach in the vanguard of the semantic approach. Specifically, the partial structures approach is considered useful in all the ways the received view is not (French & Ladyman 1999).

However, this near complete disavowal of the received view in post-positivist philosophy of science rests on a number of misconceptions, the first being the misattribution of a-prioristic convictions to the logical empiricists. Compare Carnap’s account of the nature of philosophical problems:

Thus if conventions are chosen independently of empirical considerations, they are likely to be useless. This is most radically and explicitly expressed in Carnap’s identification of a theory’s conventional component with its Carnap sentence, which is trivially true whenever the empirical component of the theory is false (Lutz 2012a: 189–190).

There are other misconceptions. Despite entrenched views to the contrary, the syntactic approach (to which the received view belongs) is not inferior to the semantic approach (Halvorson 2012, 2013; Lutz 2014c, forthcoming). The received view never demanded first-order axiomatizations (Lutz 2012c: §2) and can completely capture the formalism of van Fraassen’s approach (Lutz 2014a). In the following, I will show that it can also capture the core notions of the partial structures approach—partial truth, partial homomorphism, and partial isomorphism—because partial model theory can be captured in model theory.

2. Partial Structures and Partial Truth

The partial structures approach is motivated by a simple consideration: Scientists usually do not have wholly determined concepts or complete information about a domain, so the domain’s structure cannot be determined with arbitrary precision. For most relations, it is at best known of some tuples of objects that they fall under the relation and known of some tuples that they do not fall under it. For many tuples this is unknown (possibly because it is undetermined). Similarly, the value of many functions are not known for all possible arguments. Unlike the structures of standard model theory, partial structures are defined so as to take this lack of knowledge into account.

Assume a language \(\mathcal{L}=\{P_i\}_{i\in I}\cup\{F_j\}_{j\in J}\cup\{c_k\}_{k\in K}\), where P_i is an m_i-place relation symbol for every i ∈ I, F_j an n_j-place function symbol for every j ∈ J, and c_k a constant symbol for every k ∈ K. While most works on partial structures in the philosophy of science (e. g., da Costa & French 1990, 2000) do not consider functions, and the foundational paper by Mikenberg, da Costa, and Chuaqui (1986) does not consider constants, the respective definitions can be easily combined to give

 
Definition 1. \(\tilde{\mathfrak{A}}\) is a partial \(\mathcal{L}\)-structure if and only if

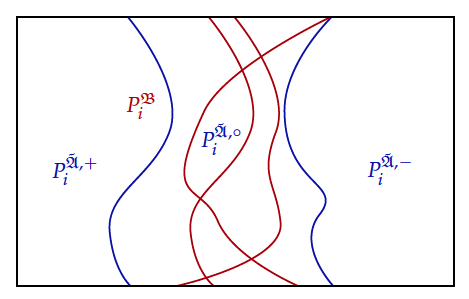
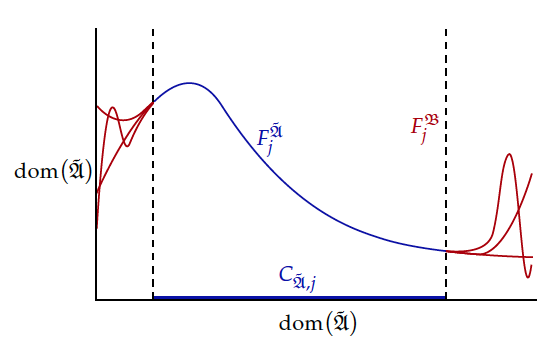
where \(P_i^{\tilde{\mathfrak{A}},+}\), \(P_i^{\tilde{\mathfrak{A}},-}\), and \(P_i^{\tilde{\mathfrak{A}},\circ}\) form a partition of \(A^{m_i}\) for each \(i\in I\),[2] \(F_j^{\tilde{\mathfrak{A}}}: C_{\tilde{\mathfrak{A}},j}\longrightarrow A\) is a function with domain \(C_{\tilde{\mathfrak{A}},j}\subseteq A^{n_j}\) for each \(j\in J\), and \(c_k^{\tilde{\mathfrak{A}}}\in A\) for each \(k\in K\).

 
In analogy to the notation in model theory (e.g., Chang & Keisler 1990), \(A\) is the domain \(\operatorname{dom}\)(\(\tilde{\mathfrak{A}}\)) of \(\tilde{\mathfrak{A}}\), \(\bigl\langle P_i^{\tilde{\mathfrak{A}},+},P_i^{\tilde{\mathfrak{A}},-},P_i^{\tilde{\mathfrak{A}},\circ}\bigr\rangle\) is the partial relation that \(\tilde{\mathfrak{A}}\) assigns to \(P_i\) for each \(i\in I\), \(F_j^{\tilde{\mathfrak{A}}}\) is the partial function that \(\tilde{\mathfrak{A}}\) assigns to \(F_j\) for each \(j\in J\), and \(c_k^{\tilde{\mathfrak{A}}}\) is the constant (the element of \(\operatorname{dom}\)(\(\tilde{\mathfrak{A}}\))) that \(\tilde{\mathfrak{A}}\) assigns to \(c_k\) for each \(k\in K\). The definition of partial structures by Mikenberg et al. (1986: def. 1) is recovered for \(K=\emptyset\), the definition by da Costa and French (1990: 255–256) for \(J=\emptyset\).[3] \(P_i^{\tilde{\mathfrak{A}},+}\) contains the known instances of \(P_i\) and \(P_i^{\tilde{\mathfrak{A}},-}\) its known non-instances. For each \(i\in I\), lack of knowledge about \(P_i\) is represented by \(P_i^{\tilde{\mathfrak{A}},\circ}\neq\emptyset\) and for each \(j\in J\), lack of knowledge about \(F_j\) is represented by proper subsets \(C_{\tilde{\mathfrak{A}},j}\subset A^{n_j}\), in which case \(F_j^{\tilde{\mathfrak{A}}}\) is a proper partial function on \(A^{n_j}\). Constant symbols are interpreted as in a structure, and thus not used to express lack of knowledge.[4]

In the partial structures approach, background knowledge is expressed by primary statements, a set \(\tilde\Pi\) of \(\mathcal{L}\)-sentences (Mikenberg et al. 1986: def. 3; da Costa & French 1990: 256). It is taken into account by the core notion of the partial structures approach:

 
Definition 2. \(\mathcal{L}\)-sentence \(\sigma\) is partially true in partial \(\mathcal{L}\)-structure \(\tilde{\mathfrak{A}}\) relative to \(\tilde\Pi\) if and only if there is an \(\mathcal{L}\)-structure \({\mathfrak{B}}\) with \(B=A\), \(P_i^{\tilde{\mathfrak{A}},+}\subseteq P_i^{{\mathfrak{B}}}\subseteq A^{m_i}\setminus P_i^{{\mathfrak{A}},-}\) for each \(i\in I\), \(F_j^{{\mathfrak{B}}}|{C_{\tilde{\mathfrak{A}},j}}=F_j^{\tilde{\mathfrak{A}}}\) for each \(j\in J\), and \(c_k^{{\mathfrak{B}}}=c_k^{\tilde{\mathfrak{A}}}\) for each \(k\in K\) (in which case \({\mathfrak{B}}\) is called an extension of \(\tilde{\mathfrak{A}}\)), such that

An extension \({\mathfrak{B}}\) of \(\tilde{\mathfrak{A}}\) is called \(\tilde{\mathfrak{A}}\)-normal if and only if \({\mathfrak{B}}\vDash\tilde\Pi\).[5]

 
The structure \({\mathfrak{B}}\) thus extends for each \(i\in I\) the partial interpretation of \(P_i\) and for each \(j\in J\) the partial interpretation of \(F_j\) to an interpretation in the sense of model theory (see Figures 1 and 2). And \(\sigma\) is partially true in \(\tilde{\mathfrak{A}}\) if and only if it is true in some extension of \(\tilde{\mathfrak{A}}\) in which the primary statements are true, that is, if and only if it is true in some \(\tilde{\mathfrak{A}}\)-normal structure. Partial truth is also called ‘pragmatic truth’ and ‘quasi truth’. One of the most important properties of partial truth is that incompatible sentences can be partially true without partial truth being trivial: Let \(\tilde{\mathfrak{A}}\) be the partial structure \(\bigl\langle A,\bigl\{\bigl\langle P_1^{\tilde{\mathfrak{A}},+},P_1^{\tilde{\mathfrak{A}},-},P_1^{\tilde{\mathfrak{A}},\circ}\bigr\rangle\bigr\},\bigl\{c_1^{\tilde{\mathfrak{A}}}\bigr\}\bigr\rangle\) with \(A=\{1,2,3\}\), \(P_1^{\tilde{\mathfrak{A}},+}=\{1\}\), \(P_1^{\tilde{\mathfrak{A}},-}=\{3\}\), \(P_1^{\tilde{\mathfrak{A}},\circ}=\{2\}\), \(c_1^{\tilde{\mathfrak{A}}}=2\), and \(\tilde\Pi=\emptyset\). Then \({\mathfrak{B}}\) can extend \(\tilde{\mathfrak{A}}\) such that \(P_1^{{\mathfrak{B}}}=\{1\}\) or \({\mathfrak{B}}\) can extend \(\tilde{\mathfrak{A}}\) such that \(P_1^{{\mathfrak{B}}}=\{1,2\}\), and thus \(P_1c\) and \(\neg P_1c\) are both partially true. But since for every extension \({\mathfrak{B}}\) it holds that \(\{1\}\subseteq P_1^{{\mathfrak{B}}}\), \(\neg\exists xP_1x\) is not partially true.

Figure 1. A partial unary relation of some partial structure \(\tilde{\mathfrak{A}}\) (blue) and three of its possible extensions (red). The area inside the black box is the domain of \(\tilde{\mathfrak{A}}\) and all its extensions.

Figure 2. A partial unary function of some partial structure \(\tilde{\mathfrak{A}}\) (blue) and three of its possible extensions (red). The horizontal and vertical black axes each correspond to the domain of \(\tilde{\mathfrak{A}}\) and all its extensions.

3. Partial Model Theory as First-Order Model Theory

4. Partial Truth as Truth of a Ramsey Sentence

So far this discussion has related partial model theory only to first order model theory. Expressing partial truth in second-order model theory, however, is particularly satisfying. Recall that we are dealing with three languages: Partial structures use language \(\mathcal{L}\), while \(\Pi\) is phrased in language \(\mathcal{L}^\ast\), which besides \(\mathcal{L}\) also contains language \(\mathcal{L}'\). If \(\mathcal{L}^\ast\) is finite, the Ramsey sentence \(\mathsf R_{\mathcal{L}'}(\sigma)\) of an \(\mathcal{L}^\ast\)-sentence \(\sigma\) is defined as \(\exists_{i\in I}X_i\exists_{j\in J}Y_j\sigma^\dagger\). To arrive at \(\sigma^\dagger\), one replaces in \(\sigma\) every relation symbol \(P_i, i\in I\), by the \(m_i\)-place relation variable \(X_i\), and every function symbol \(F_j, j\in J\), by the \(n_j\)-place function variable \(Y_j\). Thus \(\sigma^\dagger\) is a second-order \(\mathcal{L}'\)-formula, and the Ramsey sentence \(\mathsf R_{\mathcal{L}'}(\sigma)\) is a second-order \(\mathcal{L}'\)-sentence. Ramsey sentences provide a new way of formulating partial truth:

 
Claim 3. If \(\tilde\Pi\) and \(\mathcal{L}\) are finite, then \(\mathcal{L}\)-sentence \(\sigma\) is partially true in partial \(\mathcal{L}\)-structure \(\tilde{\mathfrak{A}}\) with respect to \(\tilde\Pi\) if and only if for the corresponding \(\mathcal{L}’\)-structure \({\mathfrak{A}}\) it holds that

Proof. Since \(\tilde\Pi\) and \(\mathcal{L}\) are finite, so are \(\Pi\) and \(\mathcal{L}^\ast\). Therefore, by claim 1, \(\sigma\) is partially true in \(\tilde{\mathfrak{A}}\) if and only if \({\mathfrak{A}}\) has an expansion \({\mathfrak{C}}\) such that \({\mathfrak{C}}\vDash\sigma\land\bigwedge\Pi\). Hence it has to be shown that there is such an expansion if and only if \({\mathfrak{A}}\vDash \mathsf R_{\mathcal{L}’}\bigl(\sigma\land\bigwedge\Pi\bigr)\).

‘\(\Leftarrow\)’: Since \({\mathfrak{A}}\vDash\mathsf R_{\mathcal{L}’}\bigl(\sigma\land\bigwedge\Pi\bigr)\), there is a relation \(Q_i\subseteq A^{m_i}\) for every \(i\in I\) and a function \(G_j: A^{n_j}\longrightarrow A\) for every \(j\in J\) such that \(\{Q_i\}_{i\in I}\cup\{G_j\}_{j\in J}\) satisfies \(\bigl(\sigma\land\bigwedge\Pi\bigr)^\dagger\) in \({\mathfrak{A}}\). Define \({\mathfrak{C}}\) so that \(P_i^{{\mathfrak{C}}}=Q_i\) for each \(i\in I\), \(F_j^{{\mathfrak{C}}}=G_j\) for each \(j\in J\), and \({\mathfrak{C}}|_{\mathcal{L}’}={\mathfrak{A}}\). Induction on the complexity of \(\sigma\land\bigwedge\Pi\) shows that \({\mathfrak{C}}\vDash \sigma\land\bigwedge\Pi\).

‘\(\Rightarrow\)’: Induction shows that \(\{P_i^{{\mathfrak{C}}}\}_{i\in I}\cup\{F_j^{{\mathfrak{C}}}\}_{j\in J}\) satisfies \(\bigl(\sigma\land\bigwedge\Pi\bigr)^\dagger\) in \({\mathfrak{A}}\), so that \({\mathfrak{A}}\vDash\exists_{i\in I}X_i\exists_{j\in J}Y_j\bigl(\sigma\land\bigwedge\Pi\bigr)^\dagger\).

☐

Somewhat shorter, \(\sigma\) is partially true in \(\tilde{\mathfrak{A}}\) with respect to \(\tilde\Pi\) if and only if \(\mathsf R_{\mathcal{L}’}\bigl(\sigma\land\bigwedge\Pi\bigr)\) is true in the structure corresponding to \(\tilde{\mathfrak{A}}\).

The features of partial truth that follow from definition 2 can now also be recovered from claims 1 and 3. For instance, that two incompatible sentences can both be partially true in the same partial structure follows from the fact that, given the primary statements Π, two incompatible sentences can have Ramsey sentences that are both true in a structure that corresponds to a partial structure. Claims 2 and 3 show that the central concepts of partial model theory can be expressed in second-order model theory, which allows the transfer of extant results to partial model theory. For instance, since the truth-value of a sentence of second-order logic is conserved under isomorphisms, it follows that the partial truth-value of a sentence is conserved under partial isomorphisms.[10]

5. Partial Structures and the Received View

In the new formalizations of partial truth given in claims 1 and 3, the language \(\mathcal{L}'\) is, in keeping with the basic motivation for partial structures, considered to be directly interpreted, while the interpretation of \(\mathcal{L}^\ast\setminus\mathcal{L}'=\{P_i\}_{i\in I}\cup\{F_j\}_{j\in J}\) is only given through the interpretation of \(\mathcal{L}'\) and the primary statements Π. This notion of a basic (e. g., observational) vocabulary \(\mathcal{L}'\) and an auxiliary (e. g., theoretical) vocabulary \(\mathcal{L}^\ast\setminus \mathcal{L}'\) is the basis of many analyses in the received view (Carnap 1966: §23; Hempel 1958: §2). In principle, then, all results from analyses in terms of partial structures can also be given in the received view.

One might object that the preceding results only establish that the formalism of partial structures can be captured in first and second-order model theory, but that this result in turn cannot possibly establish that the formalism of partial structures can be captured in the formalism of the received view. For according to the received view “nothing non-syntactic constitutes any theory. In particular, whatever is meant or referred to by a term or statement (i. e., the semantic aspect), it is not constitutive of theories” (Burgos 2007: 157). Hence neither first nor second-order model theory can be used in the received view.[11]

The objection relies on a misconstrual of the received view. For not only did Carnap (1939: §24) explicitly include the semantic aspect of scientific theories in his analysis, but both he and Hempel also relied on formal model theory in their discussions of scientific theories (Lutz 2012c: 92). Indeed, truth in an expansion as it is used in claim 1 is an explicit ingredient in the model theoretic semantics developed in the received view (Przełęcki 1969: Ch. 6; Andreas 2010: 532–533). And the received view’s reliance on semantics is not a particularly esoteric aspect of logical empiricism, since Suppe (1974: §II.E) explicitly discusses it in his well-known overview of the received view and even develops it into a formal account similar to the ones by Przełęcki and Andreas (Suppe 1971).[12]

Therefore claims 1, 2, and 3 not only capture the concepts of the partial structures approach in the model theory of first and, respectively, second-order logic, but also show that analyses in the partial structures approach transfer directly to the received view. For instance, the \(\mathcal{L}’\)-sentences \(\forall\bar x(P^+_i\bar x\rightarrow \neg P_i^-\bar x)\) for \(i\in I\) and \(\forall \bar x\forall y\forall\bar v\forall w(F_j^+\bar xy\land F_j^+\bar vw\land\bigwedge_{1\leq r\leq n_j} x_r=v_r\rightarrow y=w)\) for \(j\in J\), which follow from \(\Pi\), express that in a partial structure \(\tilde{\mathfrak{A}}\), \(P_i^{\tilde{\mathfrak{A}},+}\cap P_i^{\tilde{\mathfrak{A}},-}=\emptyset\) for all \(i\in I\) and \(F_j^{\tilde{\mathfrak{A}}}\) is a partial function for all \(j\in J\). Since they are therefore basic presumptions of the formalism, they are good candidates for analytic sentences in \(\mathcal{L}’\) (cf. Carnap 1952). Such a transfer of analyses promises to be particularly interesting in connection with the relation of partial truth and the Ramsey sentence, since the Ramsey sentence plays a central role in Carnap’s philosophy of science (Psillos 2000). Some analyses do not even need to be transferred, since they already have a counterpart in the received view. An example is the claim that the interpretation of a language by a partial structure “accommodates the essential incompleteness and partial nature of scientific representations” (da Costa & French 2003: 5), which “are, crucially, conceptually incomplete and open-ended” (da Costa & French 2003: 3). Expressed in \(\mathcal{L}^\ast\), the interpretation of a relation symbol \(P_i\) is given through \(\Pi\) and specifically the sentences \(\forall\bar x (P^+_i\bar x \rightarrow P_i\bar x)\) and \(\forall\bar x (P_i^-\bar x \rightarrow \neg P_i\bar x)\). Together, these sentences are equivalent to the conjunction of the sentence \(\forall\bar x(P^+_i\bar x\rightarrow \neg P_i^-\bar x)\) and the conditional definition \(\forall\bar x[P^+_i\bar x\lor P^-_i\bar x\rightarrow(P_i\bar x\leftrightarrow P^+_i\bar x)]\). The incompleteness of a relation \(P_i, i\in I\), is in a partial structure \(\tilde{\mathfrak{A}}\) expressed by \(P_i^{\tilde{\mathfrak{A}},\circ}\neq\emptyset\). Therefore \(\exists\bar x\neg(P_i^+\bar x\lor P_i^-\bar x)\) is true in the corresponding structure, which means that the conditional definition is not equivalent to a definition. Conditional definitions have already been investigated by Carnap (1936: 442–443) under the name ‘bilateral reduction sentences’,[13] where the introduction of a term by a bilateral reduction sentence is called a ‘reduction’. Carnap comes to the conclusion that

In other words, a bilateral reduction sentence, and thus a relation in a partial structure, allows for concepts that are “incomplete and open-ended” and thus “accommodates the essential incompleteness and partial nature of scientific representation”.

6. Conclusion

It is one of the presumptions of post-positivist philosophy of science that the received view is insufficient for expressing those complexities of the scientific endeavor that can be expressed in the partial structures approach. I have shown that this presumption is false because the partial structures approach itself can be expressed in the received view with the help of auxiliary vocabularies, Ramsey sentences, and bilateral reduction sentences. Van Fraassen (1980: 56) has famously and influentially argued that results expressed with these concepts are, like most results of logical empiricism, “one and all off the mark—solution to purely self-generated problems, and philosophically irrelevant.” If van Fraassen were right, claims 1–3 would establish a reductio ad empirismum logicum of the partial structures approach. But insofar as the partial structures approach has proven its merits, the inference has to go in the opposite direction: The tools developed within logical empiricism are more useful than its detractors have acknowledged.

More generally, the claims suggest that critics of the received view have conflated lack of imagination with impossibility: The partial structures approach cannot be captured in the received view by a mere calculating about with logical formulas, but capturing it is not impossible. This conflation may also underlie many criticisms of formal philosophy of science as a whole, since few features of the scientific endeavor can be formally analyzed by a mere calculating about. It might of course be that the received view (and hence, contrary to the firm belief of da Costa and French, the partial structures approach) cannot accommodate the whole variety and complexity of science. But there might then still be generalizations of the received view that can. As Shimony notes, Carnap “took particular delight in technical advances which permitted him to widen the scope of his investigation without loss of precision” (Feigl et al. 1970), and hence such generalizations would continue the logical empiricists’ research program. Post-positivist philosophy of science is positivist philosophy of science.

Acknowledgments

An earlier version of this article is part of my PhD thesis (Lutz 2012b), prepared at the Theoretical Philosophy Unit of Utrecht University, The Netherlands, and was presented under the title “Quasi-Truth as Truth of a Ramsey Sentence” at the Philosophy of Science in a Forest conference in Leusden, The Netherlands, in 2013. I thank the audience, Thomas Müller, Janneke van Lith, F. A. Muller, and two very dedicated anonymous reviewers for helpful comments, Leszek Wroński for suggesting to describe partial structures via structures in the first place, and Alana Yu for stylistic help. Research for this article has been in part supported by the Alexander von Humboldt Foundation.

References

• Andreas, Holger (2010). Semantic Holism in Scientific Language. Philosophy of Science, 77(4), 524–543. doi:10.1086/656007
• Bell, John L. and Alan B. Slomson (1974). Models and Ultraproducts: An Introduction (3rd ed.). North-Holland.
• Bird, Alexander (2014). The Historical Turn in the Philosophy of Science. In Martin Curd and Stathis Psillos (Eds.), The Routledge Companion to Philosophy of Science (2nd ed., 79–89). Routledge.
• Bueno, Otávio (1997). Empirical Adequacy: A Partial Structures Approach. Studies in the History and Philosophy of Science, 28(4), 585–610. doi:10.1016/S0039-3681(97)00012-5
• Bueno, Otávio (2000). Empiricism, Scientific Change and Mathematical Change. Studies in the History and Philosophy of Science, 31(2), 269–296. doi:10 . 1016 / S0039-3681(99)00037-0
• Bueno, Otávio, Steven French, and James Ladyman (2002). On Representing the Relationship between the Mathematical and the Empirical. Philosophy of Science, 69(3), 497–518. doi:10.1086/342456
• Burgos, José E. (2007). The Theory Debate in Psychology. Behavior and Philosophy, 35, 149–183.
• Carnap, Rudolf (1934). On the Character of Philosophic Problems. Philosophy of Science, 1(1), 5–19.
• Carnap, Rudolf (1936). Testability and Meaning. Philosophy of Science, 3(4), 420–468.
• Carnap, Rudolf (1939). Foundations of Logic and Mathematics. Foundations of the Unity of Science. Toward an International Encyclopedia of Unified Science. University of Chicago Press. References are to the two-volume edition.
• Carnap, Rudolf (1952). Meaning Postulates. Philosophical Studies, 3(5), 65–73. doi:10. 1007/bf02350366
• Carnap, Rudolf (1966). Philosophical Foundations of Physics: An Introduction to the Philosophy of Science (Martin Gardner, Ed.). Basic Books, Inc.
• Chang, Chen Chung and H. Jerome Keisler (1990). Model Theory (3rd ed.). Studies in Logic and the Foundations of Mathematics. (3rd impression). North Holland.
• da Costa, Newton C. A. and Steven French (1990). The Model-Theoretic Approach in the Philosophy of Science. Philosophy of Science, 57(2), 248–65.
• da Costa, Newton C. A. and Steven French (2000). Models, Theories, and Structures: Thirty Years On. Philosophy of Science, 67 (Proceedings), S116–S127.
• da Costa, Newton C. A. and Steven French (2003). Science and Partial Truth: A Unitary Approach to Models and Scientific Reasoning. Oxford University Press.
• Feigl, Herbert, Carl G. Hempel, Richard C. Jeffrey, Willard V. Quine, Abner Shimony, Yehoshua Bar-Hillel, ... and Wolfgang Stegmüller (1970). Homage to Rudolf Carnap. In Roger C. Buck and Robert S. Cohen (Eds.), In Memory of Rudolf Carnap: Proceedings of the Biennial Meeting of the Philosophy of Science Association (Vol. 8). Boston Studies in the Philosophy of Science. Philosophy of Science Association. D. Reidel Publishing Company.
• Fine, Kit (1975). Vagueness, Truth and Logic. Synthese, 30(3–4), 265–300. doi:10.1007/bf00485047. References are to the corrected reprint (Fine 1997).
• Fine, Kit (1997). Vagueness, Truth and Logic. In Rosanna Keefe and Peter Smith (Eds.), Vagueness. A Reader (119–150). The MIT Press.
• French, Steven and James Ladyman (1999). Reinflating the Semantic Approach. International Studies in the Philosophy of Science, 13(2), 103–121. doi:10.1080/02698599908573612
• Halvorson, Hans (2012). What Scientific Theories Could Not Be. Philosophy of Sciences, 79(2), 183–206. doi:10.1086/664745
• Halvorson, Hans (2013). The Semantic View, if Plausible, is Syntactic. Philosophy of Science, 80(3), 475–478. doi:10.1086/671077
• Hempel, Carl G. (1958). The Theoretician’s Dilemma. In Herbert Feigl, Michael Scriven, and Grover Maxwell (Eds.), Concepts, Theories, and the Mind-Body Problem (Vol. 2, 173–226). Minnesota Studies in the Philosophy of Science. University of Minnesota Press.
• Hodges, Wilfrid (1993). Model Theory. Encyclopedia of Mathematics and its Applications. Cambridge University Press. Digitally printed in 2008.
• Hyde, Dominic (1997). From Heaps and Gaps to Heaps of Gluts. Mind, 106(424), 641–660. doi:10.1093/mind/106.424.641
• Le Bihan, Soazig (2012). Defending the Semantic View: What it Takes. European Journal for Philosophy of Science, 2(3), 249–274. doi:10.1007/s13194-011-0026-6
• Leitgeb, Hannes (2011). Logic in General Philosophy of Science: Old Things and New Things. Synthese, 179(2), 339-350. doi:10.1007/s11229-010-9776-5
• Lloyd, Elisabeth A. (1988). The Semantic Approach and Its Application to Evolutionary Theory. In PSA: Proceedings of the Biennial Meeting of the Philosophy of Science Association. Volume Two: Symposia and Invited Papers (278–285). University of Chicago Press.
• Lutz, Sebastian (2012a). Artificial Language Philosophy of Science. European Journal for Philosophy of Science, 2(2), 181–203. doi:10.1007/s13194-011-0042-6
• Lutz, Sebastian (2012b). Criteria of Empirical Significance: Foundations, Relations, Applications (Doctoral dissertation, Utrecht University). Retrieved from http://philsci-archive.pitt.edu/id/eprint/9117
• Lutz, Sebastian (2012c). On a Straw Man in the Philosophy of Science: A Defense of the Received View. HOPOS: The Journal of the International Society for the History of Philosophy of Science, 2(1), 77–120. doi:10.1086/664460
• Lutz, Sebastian (2014a). Empirical Adequacy in the Received View. Philosophy of Science, 81(5), 1171–1183. doi:10.1086/677886
• Lutz, Sebastian (2014b). The Semantics of Scientific Theories. In Anna Brożek and Jacek Jadacki (Eds.), Księga pamiątkowa Marianowi Przełęckiemu w darze na 90-lecie urodzin (33–67). Nobertinum. Authoritative preprint: http://philsci-archive.pitt.edu/id/eprint/9630.
• Lutz, Sebastian (2014c). What’s Right With a Syntactic Approach to Theories and Models? Erkenntnis, 79(Suppl. 8), 1475–1492. doi:10.1007/s10670-013-9578-5
• Lutz, Sebastian (forthcoming). What Was the Syntax-Semantics Debate in the Philosophy of Science About? Philosophy and Phenomenological Research. doi:10.1111/phpr.12221
• Mikenberg, Irene, Newton C. A. da Costa, and Rolando Chuaqui (1986). Pragmatic Truth and Approximation to Truth. The Journal of Symbolic Logic, 51(1), 201–221. doi:10.2307/2273956
• Muller, F. A. (2010). Reflections on the Revolution at Stanford. Synthese, 183(1), 87–114. doi:10.1007/s11229-009-9669-7
• Przełęcki, Marian (1969). The Logic of Empirical Theories. Monographs in Modern Logic Series. Routledge & Kegan Paul/Humanities Press.
• Psillos, Stathis (2000). Rudolf Carnap’s ‘Theoretical Concepts in Science’. Studies in History and Philosophy of Science Part A, 31(1), 151–172. doi:10.1016/s0039-3681(99)00031-x
• Schimmerling, Ernest (2011). A Course on Set Theory. Cambridge University Press.
• Suppe, Frederick (1971). On Partial Interpretation. The Journal of Philosophy, 68(3), 57–76. doi:10.2307/2025168
• Suppe, Frederick (1974). The Search for Philosophic Understanding of Scientific Theories. In Frederick Suppe (Ed.), The Structure of Scientific Theories (3–241). University of Illinois Press.
• Suppes, Patrick (1968). The Desirability of Formalization in Science. The Journal of Philosophy, 65(20), 651–664. Sixty-Fifth Annual Meeting of the American Philosophical Association Eastern Division (Oct. 24, 1968).
• van Benthem, Johan (1982). The Logical Study of Science. Synthese, 51(3), 431–472. doi:10.1007/BF00485263
• van Benthem, Johan (2012). The Logic of Empirical Theories Revisited. Synthese, 186(3), 775–792. doi:10.1007/s11229-011-9916-6
• van Fraassen, Bas C. (1980). The Scientific Image. The Clarendon Library of Logic and Philosophy. Clarendon Press.
• van Fraassen, Bas C. (1989). Laws and Symmetry. The Clarendon Library of Logic and Philosophy. Clarendon Press.

Notes

1. Leitgeb (2011) and van Benthem (2012) are notable iconoclasts.

2. In the terminology of this article, the members of a partition of a set X are disjoint sets whose union is X and that, atypically, are possibly empty (cf. Schimmerling 2011: 6).

3. While da Costa and French (1990: 255) define partial structures only for relations, their further definition of partial truth presumes that partial structures can contain constants as well.

4. As an anonymous reviewer points out, there is no principled reason why constant symbols are not so used. Lack of knowledge about a constant symbol could be expressed by not assigning an interpretation to it at all. This change would only require minor modifications of definitions 2, 4, and 5.

5. If \(\tilde\Pi\) is taken to contain only the penumbral connections of a first order vague language, an \(\tilde{\mathfrak{A}}\)-normal structure is a complete extension of an \(\tilde{\mathfrak{A}}\)-structure in the sense of Fine (1975: §2). Partial truth is then subtruth (see Hyde 1997).

6. For an n-tuple \(\bar a=\langle a_1,\dots,a_n\rangle\), \(f(\bar a)=\bigl\langle f(a_1),\dots,f(a_n)\bigr\rangle\).

7. I thank an anonymous reviewer for improving my presentation of this issue.

8. The left hand side and the right hand side of the slash denote separate conjuncts of claim 2 and its proof.

9. The translation occurs in set theory, the meta-language—a translation in predicate logic, the object language, is impossible since the underlying semantics changes between partial model theory and model theory.

10. Bueno (2000: 279–280) outlines a more direct proof of this claim.

11. I thank F. A. Muller for pointing out this possible objection.

12. Although the semantics developed by Carnap, Przełęcki, Suppe, and Andreas are closely related if not equivalent, this is not completely obvious (see Lutz 2014b).

13. For bilateral reduction sentences, Carnap also demands that \(\exists\bar x(P^+_i\bar x\lor P^-_i\bar x)\), and thus \(P_i^{\tilde{\mathfrak{A}},\circ}\neq A\), be true.