Comparing Substructural Theories of Truth

2.1. Structural Rules

In this paper, I’ll work with sequent calculi to present the logics in question, since this kind of presentation allows for an easy focus on the structural properties of a logic, which will be my main topic here.

A sequent is something of the form Γ : ∆, where Γ and ∆ are multisets of formulas. A multiset is like a set, and unlike a list, in that it doesn’t care what order its members occur in: 〈A, B, A〉 is a different list from 〈A, A, B〉, but [A, B, A] is the same multiset as [A, A, B]. However, a multiset is like a list, and unlike a set, in that it does care how many times each member occurs: [A, A, B] is a different multiset from [A, B], but {A, A, B} is the same set as {A, B}. I will assume that each multiset has only finitely many members, each of which occurs only finitely many times. Sequents stand in for arguments; Γ comprises the premises of the sequent, and ∆ its conclusions.

A sequent calculus gives us rules for deriving sequents, and each calculus determines a set of derivable sequents, which I’ll call the consequence relation determined by the calculus. These rules come in two varieties: operational and structural. An operational rule is one involving certain specific vocabulary; I’ll introduce a number of them later.

Structural rules, on the other hand, don’t involve any specific vocabulary. They apply to any formulas, independent of the shape of those formulas. There are four main structural rules I’ll consider here. Two of them I will hold totally innocent;[1] I’ll present them first. Both logics to be considered in this paper include these rules without restriction:

Identity allows us to derive A : A from nowhere, for any A; it guarantees a reflexive consequence relation. (It’s often considered an axiom scheme rather than a rule; I’ll count it as a zero-premise rule for uniformity.) Weakening allows us to add whatever premises or conclusions we like to any sequent we’ve derived, and ensures that our consequence relations will be monotonic.[2]

The remaining structural rules are the ones that seem to be playing suspicious roles in the trouble for naive truth and other semantic properties:[3]

Contraction allows us to move from a sequent that uses a formula twice as a premise or a conclusion to the corresponding sequent that uses it only once. In the presence of contraction (together with certain special cases of weakening), we can replace multisets with ordinary sets in our sequents. Since much of this paper will consider the effects of dropping contraction, though, I’ll stick with multisets throughout this paper, even when contraction is in force.

Cut allows us to combine derivations in a certain way: if we can derive A as a premise in a certain context, and A as a conclusion in a certain context, then we can put those contexts together without A, and derive the result. This is a generalization of transitivity: when cut holds, the resulting logic is transitive. (Starting from the premise-sequents B : A and A : C , an application of cut yields the conclusion-sequent B : C .) The substructural logics to be considered in this paper are logics in which one of these rules is allowed to fail.

Moreover, this is the only difference between the two approaches to be considered. Structurally, the logic nc includes identity, weakening, and cut, but not contraction; while the logic nt includes identity, weakening, and contraction, but not cut.

2.2. Operational Rules

Our target logics have more than just structural rules, of course. There are also operational rules, rules that govern particular bits of vocabulary. nc and nt include the very same operational rules. I’ll keep it relatively simple here and focus on the usual suspects: negation, conjunction, disjunction, implication, and universal and particular quantification. Even with this restricted scope, though, there’s a lot going on.

Figure 1. Using W and K to collapse ⨅ and ⊗.

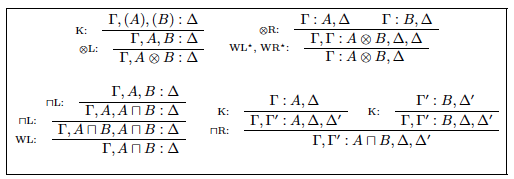
There are a variety of different ways to specify a connective like conjunction, and in the present context it’s important to be careful about the differences. We might use rules like these, taken from the calculus G1c of Troelstra and Schwichtenberg (2000). (Here and throughout, when two formulas occur in parentheses in the premise sequent of the specification of the rule, the rule can be validly applied with either (but just one!) of those formulas in the indicated place):

On the other hand, we might use rules like these:

Both ⨅ and ⊗ are recognizably conjunction-like. Moreover, in the presence of both contraction and weakening, it’s possible to show that a connective defined by the ⨅ rules will also obey the ⊗ rules, and vice versa; in fact, any such connective would exhibit exactly the behaviour of classical conjunction. See Figure 1 for the derivations.[4] (These derivations depend only on weakening and contraction; none of the other structural rules are needed.) So in any system that includes both weakening and contraction, there is usually very little reason to distinguish these two connectives, and indeed we usually do not, just thinking of them/it as conjunction.

Without contraction, though, this collapse is not possible, and ⨅ and ⊗ exhibit different logical behaviour. For example, A : A ⨅ A is derivable, but A : A ⊗ A is not. Since much of this paper will be concerned with nc, in which contraction fails, it will be important to distinguish ⨅ from ⊗. These connectives are sometimes called additive and multiplicative conjunction, respectively, and these are the terms I’ll use for them here.

Figure 2. Rules for unsplit vocabulary.

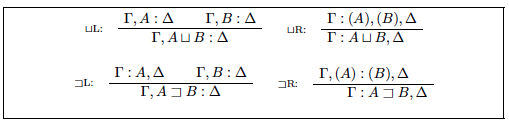
It is not just conjunction that bifurcates in the absence of contraction, however. There are additive and multiplicative versions of disjunction and implication as well. Moreover, there is a good case to be made (as in Paoli 2005) that the quantifiers ought to also bifurcate into additive and multiplicative versions, although there is no widely accepted way to do this—in particular, there is no widely accepted way to handle multiplicative quantification. (The usual quantifier rules are very much additive in their approach.)[5] I will here only use one form (the additive form) of each quantifier, then. Negation survives unsplit as well.[6] Figure 2 gives operational rules for negation and the quantifiers; operational rules for the remaining additive connectives are given in Figure 3;[7] and operational rules for the remaining multiplicative connectives are given in Figure 4.

Just as in the case of conjunction, multiplicative and additive versions of disjunction and implication collapse with each other in the presence of both weakening and contraction. As a result, although the distinction between additive and multiplicative connectives is important for understanding the noncontractive approach, it is not important at all for understanding the nontransitive approach, which allows for both weakening and contraction.

It will also help to have general vocabulary, for use when the distinction between additive and multiplicative connectives does not matter, or to make general claims about conjunctions, disjunctions, etc., when the general claims don’t depend on the difference between additive and multiplicative. It’s for this purpose that I’ve reserved more familiar logical notation; I’ll use ∧ for conjunction (⨅ and ⊗), ∨ for disjunction (⨆ and ⊕), and → for implication (⊐ and ⊸).

Figure 3. Rules for additive vocabulary

Figure 4. Rules for multiplicative vocabulary.

Both nc and nt include this full complement of operational rules, including negation, the quantifiers, and additive and multiplicative versions of the remaining vocabulary. In practice, however, the difference between additive and multiplicative vocabulary never ramifies in nt, owing to the presence of contraction, so I will stick to the general vocabulary in discussing nt.

Note that, in developing a philosophically-motivated noncontractive approach, it is open to each theorist whether to use additive vocabulary, to use multiplicative vocabulary, to pick and choose some of each, or to use the whole lot of it. Depending on theoretical goals, this decision can become interesting. For my purposes here, though, I’m using nc, in which all this vocabulary is in play; this has the disadvantage of using a lot of different symbols, but it has the advantage of not burying too much offstage.[8]

2.3. Adding Naive Truth

I’ll consider only one way of adding naive truth—adding the following two truth rules (here, T is the truth predicate, and 〈A〉 is some canonical name of A):

With these rules added, we now have complete presentations of both nc and nt. nc includes every rule examined so far other than contraction; nt includes every rule examined so far other than cut.

Both nc and nt exhibit full transparency; one can replace A with T〈A〉 or vice versa in any sequent as many times as one likes, where A appears isolated or as a subformula, without affecting derivability of that sequent. Transparent truth leads to paradoxes, and paradoxes sometimes cause trouble. For example, consider a liar sentence λ that is ¬T〈λ〉; that is, a sentence that says that it itself is not true. In the presence of the negation rules, the truth rules, identity, contraction, and cut, we can derive the empty sequent as follows:[9]

Deriving the empty sequent is bad news; in the presence of weakening it means that any sequent whatever is derivable. All arguments would be valid if this derivation were to go through. Of course, this derivation is not legitimate in either nc or nt, as it relies on both contraction and cut, and neither logic includes both of those rules.

Safety from one derivation is not a guarantee that there won’t be trouble elsewhere. However, these systems are in fact known to be safe for the truth rules; there is no derivation of the empty sequent in either of these systems.[10]

3.1. Preserving Operational Rules

The first main advantage accruing to substructural approaches is their ability to maintain, without restriction, the operational rules governing each piece of familiar logical vocabulary. As we’ve already seen, in the presence of identity, contraction, cut, and transparent truth, the negation rules suffice to cause mayhem, via the liar paradox. The conditional rules do as well; consider the following derivation, involving a curry sentence κ that is T〈κ〉 ⊸ ⊥:

We haven’t quite derived the empty sequent, but : ⊥ is bad enough; let ⊥ be something completely unacceptable—it turns out to be a theorem! Again, though, our substructural logics are safe, even with the full rules for ⊸; there is no derivation of : ⊥ in these systems either.

Things are not so simple for nonsubstructural approaches to transparent truth. Such an approach must handle the liar paradox by modifying the negation rules somehow; that’s the only remaining degree of freedom. But such a modification has nothing to say about the curry paradox, where negation is not involved. Similarly, they must handle the curry paradox by modifying the conditional rules; but this says nothing about the liar.

This leads to two problems. First, it opens the nonsubstructuralist to a familiar charge, pressed in Quine (1970), Slater (1995): the charge that they are not really addressing the paradoxes at all, but only changing the subject. After all, so the objection has it, the liar paradox we originally cared about is the one formulated with a connective ¬ obeying the negation rules. A connective that doesn’t obey the negation rules simply isn’t that same connective, no matter what symbol we use to write it. The same argument can be pressed about implication.

I don’t want to put too much weight on that objection (although I do think there might be something to it); it’s one that nonsubstructuralists have generally recognized as deserving an answer, and there are well-explored ways to answer it (for an example, see Priest 2006a: Chs. 4–5).

The real problem with having to modify the operational rules, it seems to me, is a different one entirely. It is this: the nonsubstructuralist deals with the paradoxes piecemeal, missing the general features that are allowing them to arise in the first place. But paradox runs deeper than any particular vocabulary. Tinkering with negation or conditional rules might prevent paradoxes involving negations and conditionals from arising, but it doesn’t come to grips with the general phenomenon. Two examples will reinforce this impression.

3.1.1. Validity Curry

The first comes from validity curry. I’ll follow the presentation of Beall and Murzi (2013), although see Priest and Routley (1982), Shapiro (2011), and Murzi and Shapiro (in press) for related discussion. In this paper, Beall and Murzi consider adding a validity predicate V to the object language, obeying the following two rules:

These two plausible rules are enough to derive : ⊥, given a sentence ν that is V (〈ν〉, 〈⊥〉), along with the V rules, cut, and contraction. (Slight tweaks to the curry derivation above will show how it’s done.) The nonsubstructuralist, then, must modify the V rules, using yet another finger to plug yet another hole in the crumbling dike. After all, no negation or implication occurs in the validity curry argument, so the nonsubstructuralist’s tweaks to negation and implication are beside the point here. The substructuralist, on the other hand, has already addressed this problem, since it too depends on both contraction and cut to cause trouble.

Moreover, since the substructuralist can accept these V rules along with the usual rules for the conditional, they can derive every instance of the plausible claim that valid arguments are truth-preserving. That is, they can give the following derivation for arbitrary A, B:

This derivation is available in both nc and nt, since it depends only on the truth rules and the ⊸R rule. Contraction and cut are not involved. These approaches thus avoid the argument in Field (2008: p. 284–286) against the claim that valid arguments are truth-preserving, as this argument starts from the failure of the above derivation; this failure is indeed forced on nonsubstructuralists, but not on the substructural approaches considered here.

3.1.2. Hinnion-Libert Paradox

Even if the nonsubstructuralist accepts this consequence of modifying the validity rules, however, they are still not out of the woods, as an example provided by Restall (2013) shows. Restall works in a naive set theory to develop a paradox developed in a different context in Hinnion and Libert (2003).

Using none of the operational rules we’ve seen so far, this paradox causes the same old trouble. The necessary resources are identity, contraction, cut, and the following four additional rules:[11]

The first of these rules captures part of the expected behaviour of =: when drawn on as a premise, it allows substitution of one term for another in a premise. The second and third rules capture part of the expected behaviour of set membership in a naive set theory: the claim that t is a member of the set of As can stand in for the claim that t is A, either as a premise or a conclusion. The final rule ensures that the naive theory is a naive theory of sets, by allowing us to derive the claim that t = u from t and u having the same members.[12]

From these resources, consideration of the set {x : {y : x ∈ x} = {z : ⊥}} allows for a derivation of : ⊥. (I won’t reproduce the derivation here; it’s in Restall 2013.) This paradox is in many ways just like a familiar (biconditional) curry paradox. But since it uses no conditionals and no negations, nonsubstructural approaches to paradox must deal with it separately yet again, faulting (at least) one of the four additional rules. Of course they are welcome to do so; but we can be forgiven for starting to think they are missing the point. When each new paradox must be blocked separately, it certainly gives the appearance of missing a general phenomenon.

Although I have presented the point so far as an argument against nonsubstructural approaches that preserve transparent truth, it is equally forceful against approaches to the truth-based paradoxes that work by giving up transparent truth, such as those explored in Halbach (2011), Maudlin (2004) and Scharp (2013). After all, neither validity curry nor the Hinnion-Libert paradox (nor any of the more familiar set-theoretic paradoxes) has anything at all to do with truth; playing with our theory of truth may address the liar and curry paradoxes, but it too misses the broader phenomenon.

Substructuralist approaches take a different tack entirely, and one that gets at the root of the trouble. By blocking either contraction or cut in their approach to the liar, the substructural approaches described here have already blocked the problematic derivations from validity curry or the Hinnion-Libert set.[13] There is no need for any additional work.

Rather than rushing from paradox to paradox making ad hoc modifications, these substructural approaches grapple with the paradoxes where they live: in the basic features of argumentation. This way, they can avoid having to worry about rules governing particular pieces of vocabulary; in a single fell swoop they address liars, curries, validity curries, Hinnion-Liberts, and so on.

3.2. Restricted Universal Quantification

The substructuralists’ ability to maintain familiar operational rules confers another noteworthy advantage on substructural approaches: their easy and natural treatment of restricted universal quantification (henceforth, RUQ). We’d like some way to formalize claims of the form ‘All As are Bs’. One familiar way to do this is to use the formula ∀x(Ax → Bx). So long as ∀ and → obey something like the usual operational rules, this works more or less as well as it always did (although see §4 for more discussion).

But recall that nonsubstructural approaches cannot retain the rules governing →, on pain of curry paradox. Accordingly, their account of RUQ is forced to be nonstandard as well.

I’ll use [A/B] as a noncommittal way to formulate ‘All As are Bs’. Given this, one way to look at the problem is as follows. There are a number of logical properties we’d like restricted quantification to have. Here are three:

That is: all As are As, and this should be a theorem. It should follow from At and the claim that all As are Bs that Bt. Finally, the claim that all As are Bs should entail and be entailed by the claim that there is nothing which is A and not B. Very few approaches to naive truth can yield all three of these. The kicker is the final one, which ties [A/B] to the theory of negation. By tinkering with their theory of negation, nonsubstructural approaches invariably end up somewhere that violates one of the three principles above. If they keep RUQ tied to negation via the third principle, they lose one of the others; paracomplete approaches like those in Brady (2006) and Field (2008) lose the first, and paraconsistentist approaches like those in Priest (2006b) and Beall (2009) lose the second.

In an attempt to hang on to the first and second principles, nonsubstructuralists might devise some alternate theory of RUQ. (For an attempt at this, see Beall, Brady, Hazen, Priest, and Restall 2006.) However, such an alternate theory invariably violates the third principle above, and often comes with its own additional troubles. For example, the theories developed in Beall et al. (2006) and Beall (2011) fail to validate RUQ contraposition ([A/B] : [¬B/¬A]) and vacuous quantification (¬∃xA(x) : [A/B]). Moreover, this is not an accidental failure: these principles are deliberately avoided, as they would lead to triviality in the resulting system.

Substructural theorists, on the other hand, have none of these difficulties with RUQ. nt validates all of the above desiderata directly. In nc, the situation is more textured, as there are two different ways to understand ∀x(Ax → Bx), depending on how → is read. Both of these ways validate the second principle, and the one involving ⊸ validates the first.[14] The third principle takes on more ambiguity, as ∧ must also be disambiguated. But so long as → and ∧ match (are both additive or both multiplicative), then the third principle too is validated.

Substructural approaches, then, can continue to understand [A/B] as ∀x(Ax → Bx); both nc and nt validate all three of the above principles (in the case of nc, given appropriate disambiguation), and avoid the other problematic consequences mentioned above.

4.1. Classical Logic

Classical logic has got some things going for it. Among other things, it is simple, powerful, and time-tested. For at least some purposes, it would be nice to be able to use classical logic, to get some of these advantages.[15] Here we find what is probably the most striking difference between the two approaches; at least some of the other differences to be pointed to below depend on this one.

Every classically-valid argument is valid in nt, no matter whether the classical connectives are understood as additive, multiplicative, or any combination of these; this holds for the full language, including arguments involving the transparent truth predicate. This gives a sufficient condition for nt validity that is easy to work with; it is a sufficient condition I’ll lean on repeatedly in what follows. (It is only a sufficient condition, and not also necessary, because nt includes the naive truth rules, and so validates arguments like T〈A〉 : A that are not valid in plain classical logic.) This is possible because the rule of cut is admissible in the presentation of classical logic that underlies nt. That is, any argument that can be shown to be classically valid by using the rule of cut can also be shown to be classically valid without using the rule. Since no argument depends on cut for its classical validity, all classically-valid arguments remain valid even when cut is dropped. (For more details, see Ripley 2013a; 2013b.)

The same is not true of noncontractive systems. For example, the sequents A : A⊗A and A⊕A : A are not derivable without contraction, but their classical counterparts A : A ∧ A and A ∨ A : A are surely classically valid. Moreover, this is crucial to the noncontractivist’s success in avoiding derivations of the empty sequent; adding sequents like these to a noncontractive system would (together with cut) reinstate a variant of the liar derivation considered in §2.3. A noncontractive treatment of liar sentences requires them to be treated as counterexamples to these classically-valid arguments.

On the other hand, noncontractive approaches do allow for derivation of A : A ⨅ A and A ⨆ A : A, which have the same classical counterparts as the above. Appeals to these sequents, and others like them, give noncontractivists resources to insist on an important sense in which classical logic is present in their approach. For example, Mares and Paoli (2014) point out that, if we stick to a language without quantifiers, the classically-valid arguments are precisely those that are valid-on-some-disambiguation in a system like nc, where the disambiguation in question is between additive and multiplicative. Because of this, Mares and Paoli argue, their noncontractive approach is not logically revisionary, or at least not in a bad way; every classically-valid argument is valid on some disambiguation (into additive and multiplicative), even if not on every disambiguation.

If this response can be made to fly for the full language, it would lessen the sting of any charge that noncontractivists are too logically revisionary. This would require what we do not have: a theory of additive and multiplicative quantification for which the analogous claim can be sustained.[16] Although we do not know that such a thing cannot be found, until we have one this response to the charge of unnecessary revision is at best incomplete.

Moreover, making this response of course depends on actually having the full complement of additive and multiplicative connectives (and eventually quantifiers) in the language, which only some proponents of noncontractive approaches want. For example, Zardini (2013) argues for doing without additives entirely, while Brady (2006: 34–35) argues against including multiplicative conjunction. Zardini’s restriction is optional, from a paradox-blocking point of view. But Brady’s is not; Brady’s favored set theory would be rendered trivial if multiplicative conjunction were added to the language. (See Routley et al. 1982: 366-367 for the argument, credited there independently to Dunn and Slaney.) Multiplicative disjunction, in particular, is often missing from noncontractivist proposals; for example, neither Shapiro (2015) nor Beall and Murzi (2013) makes any allowance for it.

For now, then, proponents of noncontractive approaches are recommending deviations from classical logic on a broader scale than are proponents of the nontransitive approach considered here, and for many such approaches this will remain the case. (There is nothing to prevent a proponent of a nontransitive approach from deviating further than nt does; for examples, see Tennant (1987), Weir (2015), and Thomas (2015). But such further deviation is not forced, as it is for the noncontractivist.)

Of course, neither a noncontractive nor a nontransitive approach allows for all the behaviour we are used to in classical settings; both cut and contraction have been taken to be part of the very definition of a consequence relation by a number of authors, for example Humberstone (2012), and so any substructural approach must obviously fail to be fully logically conservative. If conservativity is seen as a desideratum for theory change, as it often is (e.g., Quine 1951; Sklar 1975; Lycan 1988), then this is some drawback.

The extent of the drawback, though, can be minimized by the nontransitivist. Whatever deviations from received logical wisdom are involved in adhering to nt or its relatives, they do not involve declaring any classically-valid arguments to be invalid. As such, no restriction of classically-endorsed reasoning patterns is needed, on such a view. To the extent that we value avoiding such restrictions, then, there is some reason to prefer a nontransitive approach to a noncontractive one.

4.2. Varieties of Modus Ponens

Zardini (2013) clearly distinguishes between a variety of principles which can be taken to answer to the name modus ponens. Neither the noncontractivist nor the nontransitivist can accept all of these principles. In this subsection, I’ll quickly outline the situation; as modus ponens is important for reasoning, substructuralists of both stripes must take real care here.

4.2.2. Modus Ponens as an Argument

Next, we have single-premise arguments, of the form A ∧ (A → B) : B. Again, the nontransitive approach has only one such argument, and, since the argument is classically valid, it’s valid on the nontransitive approach as well. There are four such arguments on a noncontractive approach: the two involving ⊗ are valid, and the two involving ⨅ are invalid. Again, the problem is that additive conjunction will only allow its conjuncts to interact with each other in the presence of contraction.

Third, there are two-premise arguments, of the form A, A → B : B. Again, the nontransitive approach sees one argument, and validates it. A noncontractive approach is now down to two readings, since there is only one connective in play. Both of these readings are derivable for the noncontractivist:

So far, then, all the versions we’ve seen of modus ponens are valid on the nontransitive approach, while a noncontractive approach must take a bit more care. While either version of the two-premise modus ponens is valid on a noncontractive approach, the other versions have both valid and invalid forms. However, since each version has valid forms, the noncontractivist who wants to defend modus ponens in certain cases can always insist that those cases are to be read in one of the ways that makes modus ponens valid, unless there is some other reason to suspect this claim.

To the (perhaps limited) extent that we want to choose some particular version of modus ponens to be the “real” modus ponens, I think it’s most plausible to choose the two-premise form: this is the form that focuses directly on the conditional, and doesn’t muck about with conjunctions. After all, modus ponens is most standardly thought of as a principle governing (certain) conditionals, not governing the interaction of conditionals and conjunctions, and it’s the two-premise argument form that allows this to shine through. From this point of view, both the nontransitivist and the noncontractivist validate the “real” modus ponens; there is not much to choose between them here.

4.2.3. Modus Ponens as a Metainference

But there’s more to modus ponens than this: there are metainferential versions of modus ponens as well. These are not arguments at all, but rather sequent rules connecting some valid arguments to others. I’ll consider two forms here, which I’ll call context-sharing and context-free metainferential modus ponens (CSMMP and CFMMP, respectively).[17]

Of course, each of these forms comes in two versions for the noncontractivist, depending on which → is used. In this case, though, both conditionals give the same result: CFMMP is derivable in nc, for both ⊐ and ⊸, and CSMMP must be rejected. (More on this rejection of CSMMP presently.) So the division between CSMMP and CFMMP looms large for the noncontractivist whichever conditional is in play.

For the nontransitivist, on the other hand, these two rules stand or fall together, as they are derivable from each other in the presence of weakening and contraction. As it happens, they must fall. As is pointed out in Negri and von Plato (2001: 19), CFMMP brings almost every instance of cut with it, given ⊸R—all that is needed is that ∆′ is nonempty; that is, that ∆′ = ∆″, δ for some formula δ. Then we have the following derivation:

But this is far too much cut to be tolerated by a proponent of nt or its relatives; the restriction to nonempty ∆′ is hardly a restriction at all.[18] Similarly, with cut in hand it is quick to derive full CFMMP (for ⊸, this requires in addition Id and ⊸L; for ⊐, it takes Id, K, and ⊐L). So, for the nontransitivist, MMP (in both forms) must go; it is basically cut in disguise.

As a defender of a nontransitive approach, I find it tempting at this point to make an argument along the following lines: “Sure, I’ve got to reject MMP. But we can see it’s almost equivalent to cut, so this is no additional problem for my view. Whatever is allegedly wrong with rejecting MMP must already be wrong with rejecting cut.” I’ve come to think, though, that this kind of response is at best only half-fair. It’s true that rejecting MMP is no worse of a problem than rejecting cut is, since they’re more or less equivalent to each other. But Zardini (2013) argues that this rejection of CFMMP is a real problem. If this is right, there’s a real problem with rejecting cut. It doesn’t have to be a problem over and above itself in order to be a problem!

Zardini argues as follows:

For the logical idea of modus ponens can be seen as intimately connected with and arguably grounded in the semantic idea that a true conditional cannot have a true antecedent and an untrue consequent; yet, on the strategy under consideration, since : T〈κ〉 → ⊥ and : T〈κ〉 hold, we’re presumably asked to accept that they are true (and, given other details of the theory, false), while ⊥ is untrue. So we’re in effect asked to reject the idea that a true conditional cannot have a true antecedent and an untrue consequent. This is not only in itself rebarbative; as I’ve just indicated, it also means to reject the very semantic idea with which modus ponens is intimately connected and in which it is arguably grounded. (2013: 579)[19]

I agree with Zardini that a true conditional cannot have a true antecedent and an untrue consequent.[20] But I certainly don’t accept that this claim is what grounds modus ponens. On my view, this claim is well downstream of the real action.

Arguments are in the first place about connections between premises and conclusions, not connections between conclusions and conclusions. What matters for modus ponens is the fact that B validly follows from the premises A and A → B. (On the account of consequence I endorse in Ripley (2013a), this is in turn grounded in certain of our conversational norms: someone who has asserted both A and A → B, but who has also denied B, has violated these norms.) From that two-premise version, MMP follows only via cut. When cut fails, there too MMP can fail. But the core of modus ponens—its two-premise version—is never threatened. Nor are the formulations that make the two-premise version explicit, in the sense of Brandom (1994): the one-premise and single-sentence versions.

For some, this might be a bridge too far. I don’t reckon it’s much of a problem at all, myself; and neither should Zardini. Although Zardini accepts CFMMP, he must reject CSMMP, as must all noncontractive theorists. After all, in the presence of CSMMP and cut, there is simply no need for contraction to produce troublesome results from a curry sentence κ that is T〈κ〉 ⊸ ⊥.[21] Consider the following derivation:[22]

Call this derivation δ₁. Then we have:

This is why noncontractivists cannot accept CSMMP. But note that CSMMP simply says that the consequences of any Γ are closed under modus ponens. This means that, although the theorems in noncontractive systems can be closed under modus ponens, the consequences of particular premises need not be, and in some cases had better not be. That is, when reasoning about what follows from premises Γ, noncontractivists like Zardini must allow that, in such a situation, A and A ⊸ B might both follow, without B following.

When it comes to closure under modus ponens, then, the only difference between our views is that I think this can happen for empty Γ and Zardini thinks it cannot. But once you’re happy for such a thing to happen at all, I find it very hard indeed to see why it would be important to resist the special case where Γ happens to be empty.

One might worry that nt has gone too far here, that without CSMMP or CFMMP or some relative, conditionals are too close to idle. They might ‘work’ as premises, as the argument versions of modus ponens show, but they don’t seem to ‘work’ as conclusions; once concluded, conditionals seem just to sit there! But this worry would be misplaced. The following rule is admissible in nt:

Conditionals, as conclusions, have the same force that validity itself has. (Conditionals make validity explicit, again in the sense of Brandom (1994).) And validity is surely not idle: as above, I reckon its force is to rule out asserting the premises while denying the conclusions; this is a substantive restriction. So even as conclusions, conditionals are far from idle in nt.

When it comes to modus ponens, then, the situation between the noncontractivist and the nontransitivist is textured. The nontransitivist can accept any sentence-level or argument-level formulation of modus ponens you like, but must reject both CSMMP and CFMMP. The noncontractivist, on the other hand, needs to take care about conjunction in sentence-level and some argument-level formulations of modus ponens, and must also reject CSMMP, but can accept CFMMP. There is of course room to worry that rejecting CSMMP, as both the noncontractivist and the nontransitivist do, makes for serious trouble with substructural views entirely. CSMMP is, after all, nothing more than a guarantee that theories are closed under modus ponens, which might seem like a natural desideratum. If this is trouble, it is trouble shared by the noncontractivist and the nontransitivist. (See §4.4.1 for discussion of a related issue.)

4.3. Conditional Contraction and RUQ

Consider a sequent of the form A → (A → B) : A → B; call this conditional contraction (to contrast with the rule of structural contraction, which we’ve been considering throughout).[23] The nontransitive approach sees essentially one sequent here, and validates it (since it’s classically valid). A noncontractive approach, as you’d expect by now, makes eight readings available.

Of the eight, three are valid on a noncontractive approach: A ⊐ (A ⊐ B) : A ⊐ B; A ⊐ (A ⊐ B) : A ⊸ B; and A ⊐ (A ⊸ B) : A ⊸ B. The other five are invalid. Since ⊐ is very rarely used in noncontractive theories, these can seem more like curiosities than anything. Conditional contraction, for most noncontractive theorists, simply fails. Because of this, for much of this section I will treat the noncontractive approach as though it used ⊸ exclusively. It will not come out well for such an approach. But I don’t take this to provide an argument against a noncontractive approach in general. Rather, I take it to provide an argument that, at least sometimes, a noncontractivist should acknowledge and make use of ⊐.

Conditional contraction has been held responsible for much mischief among nonclassical logicians concerned with paradox. (For details, see Restall 1993; 1994.) In particular, together with modus ponens and conditional identity (that is, : A → A) it seems to play an important role in many formulations of curry paradox. For this reason, a number of different proposals for dealing with paradox, substructural and nonsubstructural alike, hinge in part on doing without conditional contraction, or at the very least on distinguishing two different conditionals, one of which obeys modus ponens and conditional identity but not conditional contraction, and the other of which obeys conditional contraction but not both modus ponens and conditional identity.[24]

Most often, the reasons given for rejecting conditional contraction are flatly ad hoc: together with modus ponens and conditional identity, it seems to doom us to curry-flavoured disaster, but modus ponens and conditional identity are intuitively better-supported than conditional contraction. Thus, it is often thought, if one of them has to go, it should be conditional contraction. This has all the charm of thumbscrews: it may convince some to submit, but it does nothing to help us accustom ourselves to the situation.[25]

Complicating matters, it can be tricky to trust our intuitions about a connective like →. This is because there are compelling and familiar reasons to take →, in any of its manifestations here (and in many other places besides), to be a terrible model for natural language conditionals.[26] As such, we shouldn’t form strong views as to which →-involving arguments ought to be valid based on natural-language conditional-involving arguments. Whatever → is good for, it isn’t that.

We looked above, though, at one of the things that → is good for: restricted universal quantification. If we understand [A/B] as ∀x(Ax → Bx), as is traditional, then conditional contraction amounts to RUQ contraction: [A/[A/B]] : [A/B]. In words, this is the argument from “All As are such that all As are Bs” to “All As are Bs”. No theory of RUQ cited above includes this principle, as, together with the other desiderata, it leads to an RUQ-based variant of curry paradox. In fact, avoiding the validity of RUQ contraction is one of the main desiderata sought in Beall et al. (2006), for just this reason.

This kind of approach, though, must grapple with the following concerns. Imagine having to decide whether all As are Bs. Well, if all As are such that all As are Bs, then, it would seem, that’s that: the As have spoken, and nothing else has any claim to mattering. That is, if it’s not the case that all As are Bs, then there must be a counterexample, and if there’s a counterexample it must be among the As; if they’re all such that all As are Bs, then indeed all As are Bs. Those approaches to RUQ that have avoided RUQ contraction (such as Beall et al. 2006; Beall 2009; Field 2008; 2014) have not alleviated this impression.[27]

By failing to derive conditional contraction, then, a noncontractive approach can face difficulty in its theory of RUQ. Because of this, I would heartily commend ⊐ to noncontractivists for purposes of RUQ. Noncontractivists should understand [A/B] as ∀x(A(x) ⊐ B(x)) instead of ∀x(A(x) ⊸ B(x)). This shift to ⊐ restores RUQ contraction. There is a minor difficulty with the desiderata of §3.2 for the noncontractivist even here, as they will no longer validate : [A/A] on such an approach, but only the weaker : [A/A], [A/A]. I reckon this is a small price to pay. (The situation is the same—and for the same reasons—with the additive law of excluded middle: : A ⨆ ¬A, A ⨆ ¬A is derivable in nc, but : A ⨆ ¬A is not. Noncontractivists who are comfortable there should have no trouble here.)

The nontransitive approach, of course, validates both conditional and RUQ contraction without any fuss, as well as : [A/A], as all of these are classically valid. When it comes to RUQ, then, I reckon that nt slightly outperforms nc.

One might think that, just as a noncontractive approach can face difficulty with RUQ contraction, that the nontransitive approach faces a similar difficulty with RUQ-based expressions of transitivity. (Something like this worry has been expressed to me in conversation by both Jc Beall and Elia Zardini, independently.) This, though, is not the case. If there is an RUQ-based expression of transitivity, it is presumably the sequent [A/B], [B/C] : [A/C]; in words, the argument from “All As are Bs” and “All Bs are Cs” to “All As are Cs”. This is a compelling argument; if the nontransitive approach had to reject the validity of this argument, that would indeed be a problem parallel to the noncontractivist’s rejection of RUQ contraction.

But the nontransitive approach is under no such obligation; this sequent is perfectly derivable, understanding [A/B] as above. After all, it is certainly classically derivable, and, as we’ve seen, everything classically derivable is also derivable for the nontransitivist. So there is no comparable RUQ-based difficulty for the nontransitivist.

4.4. Cumulative Reasoning

Here is a familiar picture of how to come to know more and more via deduction. Take Alice. She starts from some stock of premises. From these, she draws certain conclusions (step one). Then she adds these conclusions to her original premises, generating an expanded stock (step two). With this expanded stock in hand, she repeats the process, for as long as she cares to. Call this way of reasoning cumulative reasoning; it allows Alice to accumulate a larger and larger stock of knowledge as she goes. At first blush, it might seem that, so long as we stick to deductive argument, the only way for cumulative reasoning to go wrong is in step one: Alice might draw a conclusion that doesn’t really follow from her premises. As long as her conclusions actually do follow, we might think, there can be no risk introduced by step two. She can expand her stock of premises in this way without risk.

The noncontractivist and the nontransitivist alike must reject this first-blush impression, although for different reasons. For the noncontractivist, Alice might have used up some of her initial premises in reaching these conclusions; these used premises cannot be retained for future reasoning, as this would allow for them to be used twice.[28] For the nontransitivist, on the other hand, there is risk in using conclusions as premises for further reasoning, as this amounts to assuming transitivity.

Let’s look at a pair of examples. These examples involve paradox, where noncontractive and nontransitive approaches reveal their respective nonstandardnesses. The noncontractive case first: Suppose Alice begins with the single premise ‘The curry sentence is true’. From this premise, she concludes ‘If the curry sentence is true, then ⊥’, by disquoting. Then she adds this conclusion to her stock of premises. Now she has a conditional and its antecedent among her premises, so she validly concludes ⊥, by modus ponens. According to the noncontractivist, something must have gone wrong, since they insist that ⊥ does not validly follow from ‘The curry sentence is true’. Alice’s mistake, they will say, was in retaining her initial premise after she had already drawn on it: this is not always safe, and here it’s gone awry.

According to the nontransitivist, on the other hand, ⊥ does follow validly from ‘The curry sentence is true’. As such, although Alice may have made a mistake in her reasoning in the above example (adding a conclusion to her premises), this mistake didn’t lead her astray. She could have reached the same conclusion from her premise directly, without reasoning cumulatively at all.

To see the nontransitivist’s concern, we need a different example. In this second example, Alice begins with no premises at all. By nontransitivist lights, ‘The curry sentence is true’ follows validly from no premises; it is a theorem. But suppose Alice were to take this valid conclusion and add it to her stock of premises. Then, since this claim entails ⊥, she could immediately conclude ⊥. Since ⊥ does not follow from no premises (all are agreed), something must have gone wrong here; the nontransitivist will say it was Alice’s using a conclusion as a premise.

So neither the noncontractivist nor the nontransitivist can fully approve of cumulative reasoning. They diagnose different problems with it, and quarrel with different instances, but to the extent that cumulative reasoning is nonnegotiable, both noncontractive and nontransitive approaches are simply ruled out.

Each, of course, will have replacements to offer. The noncontractivist can offer a version of cumulative reasoning that is very careful about just which premises are appealed to where, making sure to discard everything that has been reasoned from, but able to retain whatever has been reasoned to most recently. The nontransitivist, on the other hand, can offer full cumulative reasoning in cases where cut is eliminable (which is almost always, but crucially not always); in these cases, they see cumulative reasoning as a safe shortcut to places that could in principle be reached in a more roundabout way. Whether either of these can fill all the purposes for which we want cumulative reasoning, and whether all those purposes are themselves legitimate, are issues I won’t enter into here.

4.4.1. Cautious Cut

It’s interesting that neither the noncontractivist nor the nontransitivist can trust cumulative reasoning, since, at least at first glance, cumulative reasoning can seem to have much more to do with transitivity than it does with contraction. This is not a coincidence. In this section, I’ll examine the property of cautious cut, which is distinct from cut. It will emerge that both the nontransitivist and the noncontractivist must avoid cautious cut; it would trivialize either approach. But it is cautious cut, not cut, that has the best claim to the intuitive motivation for transitivity. I conclude that, in addition to giving up contraction, noncontractive views don’t even get to keep the kind of transitivity worth wanting.

The reason for the importance of cautious cut is that it is in this form that transitivity connects with cumulative reasoning. A consequence relation obeys cautious cut iff whenever Γ : A and Γ, A : B are valid, then so too is Γ : B. The connection to cumulative reasoning should be apparent: reasoning cumulatively, if A validly follows from Γ, and B validly follows from Γ together with A, then we can conclude A from Γ, add it to Γ to reach B, and then take ourselves to have reached B from Γ. Cautious cut is more usually studied in relation to nonmonotonic logics, but it turns out to matter here as well. Both noncontractive and nontransitive approaches must reject it; the problems already discussed for cumulative reasoning apply directly to cautious cut.

Note that cut proper, as presented in §2.1, is independent of cautious cut, at least in the absence of contraction. In the presence of contraction, on the other hand, cut entails cautious cut.[29] As we’ve seen, both the noncontractive and the nontransitive approaches must reject cautious cut; the only way to retain cut, then, is to reject contraction.

But why should we want to retain cut? Arguments in favour of cut itself tend to proceed by pointing to the value of cumulative reasoning: that is, they are in the first instance arguments for cautious cut. For example, Boolos (1984: 377) says that the presence of cut ‘permits the development and utilization within derivations of subsidiary conclusions, or, as they would be called in a more informal setting, lemmas.. . . Sustained ordinary reasoning cannot be carried on in a [system without cut], where we are unable to appeal to previously established conclusions’.[30]

Boolos was considering systems in which contraction is implicit, and so he had little reason to distinguish cut from cautious cut. But we can see that his argument applies in the first place to cautious cut, and only derivatively, if at all, to cut proper. Sustained ordinary reasoning, where it involves lemmas, involves them on the model of cumulative reasoning: as things that, once established, can be drawn on repeatedly in combination with any other available information, including the very information appealed to in establishing them. Neither the nontransitive nor the noncontractive approach can accommodate this in the obvious way; both owe a story about the failure of this important transitivity property. But this threatens to undercut any motivation the noncontractivist can offer for retaining cut: without cautious cut, what’s so important about cut itself ?

There might be some temptation, on the part of the noncontractivist, to claim that cautious cut is not a pure transitivity property, because it involves some admixture of contraction. One hears claims like this all the time in informal discussions; and although it is often unclear exactly what they amount to, they are far from meaningless. I will consider three ways of understanding this objection; none of them, I think, should convince us that the noncontractivist can dodge the present worry.

First, if the objection is understood merely as the claim that noncontractivists must reject cautious cut in order to avoid triviality, then it’s hardly an objection at all—it’s my point, and the source of the present worry.

Perhaps, though, the objector means to point to the fact that two copies of Γ come into an application of cautious cut, one in each premise-sequent, but that only one copy of Γ comes out in the conclusion-sequent. This two-to-one move of course smells like contraction—Γ must be used twice in the premise-sequents (once in each sequent), while only a single use is recorded in the conclusion-sequent. But a quick glance at the noncontractivist’s two-premise rules for the additive connectives reveals that they all exhibit this exact feature. So a two-to-one move of this sort, despite its odour, does not necessarily involve smuggling in any contraction.

Third, the objector might mean to claim that contraction follows from cautious cut, or at least that some important instances of it do. I think this is the most charitable reading to give to the objection. Consider the following move:

This is an instance of cautious cut, and its first premise-sequent is always valid (given reflexivity and weakening). So, by using cautious cut, we can always move from Γ, A, A : B to Γ, A : B, and that’s enough contraction to cause trouble for the noncontractivist.

Again, though, this is less an objection than it is my point. The best-motivated kind of transitivity, motivated by considering its role in ‘sustained ordinary reasoning’, is not cut at all, but cautious cut. Since it turns out that cautious cut brings with it a wide range of instances of contraction, it follows that respecting transitivity brings with it this same wide range.

So the best-motivated kind of transitivity must go, for both the nontransitivist and noncontractivist, and go it shall. But having gotten rid of cautious cut, there isn’t much value left in retaining cut itself. Better to follow through on the rejection of all forms of transitivity and be done with it.

This argument cannot be turned around. The most natural motivations for contraction are motivations for contraction proper; there is no better-motivated relative of contraction not open to the nontransitivist.